Fractals
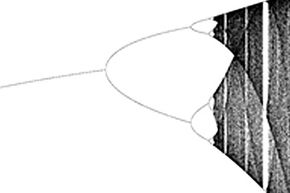
If you examine a bifurcation diagram closely, you begin to see interesting patterns. For example, start with a completed diagram, such as the one in the first picture.
Next, zoom in on the first doubling point. It looks like a rounded, sideways V. Now look at the smaller, sideways V's that come next in the series.
Advertisement
Now zoom in again, say, on that upper, smaller V.
Notice how this region of the diagram looks like the original. In other words, the large-scale structure of the figure is repeated multiple times. The doubling regions exhibit a quality known as self-similarity -- small regions resemble large ones. Even if you look in the chaotic areas of the diagram (which occur to the right), you can find this quality.
Self-similarity is a property of a class of geometric objects known as fractals. The Polish-born mathematician Benoît Mandelbrot coined the term in 1975, after the Latin word fractus, which means "broken" or "fragmented." He also worked out the basic math of the objects and described their properties. In addition to self-similarity, fractals also possess something known as fractal dimension, a measure of their complexity. The dimension is not an integer -- 1, 2, 3 -- but a fraction. For example, a fractal line has a dimension between 1 and 2.
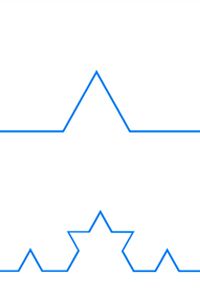
The Koch snowflake -- named after the Swedish mathematician Helge van Koch -- stands as a classic example of a fractal. To derive the shape, van Koch established the following rules, first for a line:
- Divide a line segment into three equal parts
- Remove one-third of the segment out of the middle
- Replace the middle segment with two segments of the same length such that they all connect
- Repeat indefinitely on each line segment
The second picture shows what the first two iterations would look like:
If you start with an equilateral triangle and repeat the procedure, you end up with a snowflake that has a finite area and an infinite perimeter:
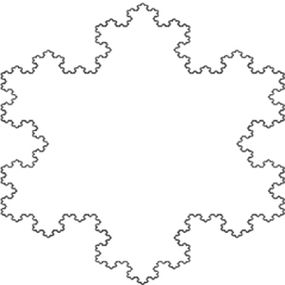
Today, fractals form part of the visual identity of chaos. As infinitely complex objects that are self-similar across all scales, they represent dynamical systems in all their glory. In fact Mandelbrot eventually proved that Lorenz's attractor was a fractal, as are most strange attractors. And they're not limited to the ruminations of scientists or the renderings of computers.
Fractals are found throughout nature -- in coastlines, seashells, rivers, clouds, snowflakes and tree bark. Before you take a field trip, however, be aware that self-similarity behaves a little differently in natural systems. In controlled mathematical environments, an object with self-similarity often displays an exact repetition of patterns at different magnifications. In nature, patterns obey statistical self-similarity -- they don't repeat exactly but parts of them show the same statistical properties at many different scales.