How the Doppler Effect Works

Let's begin our dissection of the Doppler effect by considering a source that creates waves in water at a certain frequency. This source produces a series of wave fronts, with each moving outward in a sphere centered on the source. The distance between wave crests -- the wavelength -- will remain the same all the way around the sphere. An observer in front of the wave source will see the waves equally spaced as they approach. So will an observer located behind the wave source.

Now let's consider a situation where the source is not stationary, but is moving to the right as it produces waves. Because the source is moving, it begins to catch up to the wave crests on one side while it moves away from the crests on the opposite side. An observer located in front of the source will see the crests all bunched up. An observer located behind the source will see the waves all stretched out. Remember, the frequency equals the number of waves that pass a specific point per second, so the observer in front actually sees a higher frequency than the observer in back of the source.

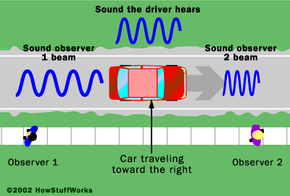
The scenario above describes waves formed in water, but it also applies to sound waves and light waves. Sound waves are heard, not seen, so the observer will hear the bunched-up waves as a higher-pitched sound, the stretched-out waves as a lower-pitched sound. For example, consider a car traveling down a highway between two observers, as shown below. The roar of the engine and friction between the tires and the road surface create a noise -- vroom -- that can be heard by both observers and by the driver.

To the driver, this noise will not change. But the observer located in front of the car will hear a higher-pitched noise. Why? Because the sound waves compress as the vehicle approaches the observer located in front. This increases the frequency of the wave, and the pitch of the vroom rises. The observer located behind the car will hear a lower-pitched noise because the sound waves stretch out as the car recedes. This decreases the frequency of the wave, and the pitch of the vroom falls.

Light waves are perceived as color, so the observer will sense the bunched-up waves as a bluer color, the stretched-out waves as a redder color. For example, consider an astronomer observing a galaxy through a telescope. If the galaxy is rushing toward Earth, the light waves it produces will bunch up as it approaches the astronomer's telescope. This increases the frequency of the wave, which shifts the colors of its spectral output toward the blue. If the galaxy is rushing away from Earth, the light waves it produces will spread apart as it recedes from the astronomer's telescope. This decreases the frequency of the wave, which shifts the colors of its spectral output toward the red.

As you can imagine, astronomers routinely take advantage of the Doppler effect to measure the speed at­ which planets, stars and galaxies are moving. But its usefulness isn't limited to outer space. Doppler's discovery is integral to several applications right here on Earth.