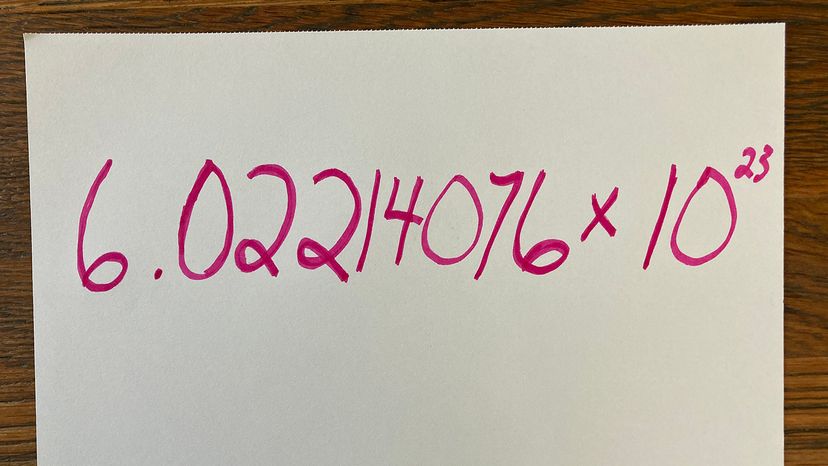
We'll give you a hint: It's not 867-5309. That's Jenny's number, not Avogadro's. You're also not going to find these digits scrawled in marker on the wall of the public bathroom. You will, however, discover it within the pages of a standard chemistry textbook: It's 6.02214076 × 1023. Written out, that's 602,214,076,000,000,000,000,000 [source: NIST]. Short on time? Just call it a mole.
Just like a dozen is 12 things, a mole is simply Avogadro's number of things. In chemistry, those "things" are atoms or molecules. In theory, you could have a mole of baseballs or anything else, but given that a mole of baseballs would cover the Earth to a height of several hundred miles, you'd be hard-pressed to find good practical use for a mole of anything bigger than a molecule [source: Hill and Kolb]. So if the mole is only used for chemistry, how did Amedeo Avogadro (full name: Lorenzo Romano Amedeo Carlo Avogadro) and chemistry cross paths?
Advertisement
Born in Italy in 1776, Avogadro grew up during an important period in the development of chemistry. Chemists like John Dalton and Joseph Louis Gay-Lussac were beginning to understand the basic properties of atoms and molecules, and they hotly debated how these infinitesimally small particles behaved. Gay-Lussac's law of combining volumes particularly interested Avogadro. The law stated that when two volumes of gases react with one another to create a third gas, the ratio between the volume of the reactants and the volume of the product is always made of simple whole numbers. Here's an example: Two volumes of hydrogen gas combine with one volume of oxygen gas to form two volumes of water vapor (at least when temperatures are high enough) with nothing left over, or:
2H2 + O2 --> 2H2O
Tinkering around with the implications of this law, Avogadro deduced that in order for this to be true, equal volumes of any two gases at the same temperature and pressure must hold an equal number of particles (Avogadro's law). And the only way to explain that this law could be true for any example, including the one we just mentioned, is if there was a difference between atoms and molecules and that some elements, like oxygen, actually exist as molecules (in oxygen's case, O2 rather than simply O) Granted, Avogadro didn't have words like "molecule" to describe his theory, and his ideas met resistance from John Dalton, among others. It would take another chemist by the name of Stanislao Cannizzaro to bring Avogadro's ideas the attention they deserved. By the time those ideas gained traction, Avogadro had already passed away.
So where does Avogadro's number fit into this? Because Avogadro's law proved so critical to the advancement of chemistry, chemist Jean Baptiste Perrin named the number in his honor. Read on to see how chemists determined Avogadro's number and why, even today, it's such an important part of chemistry.
Advertisement


