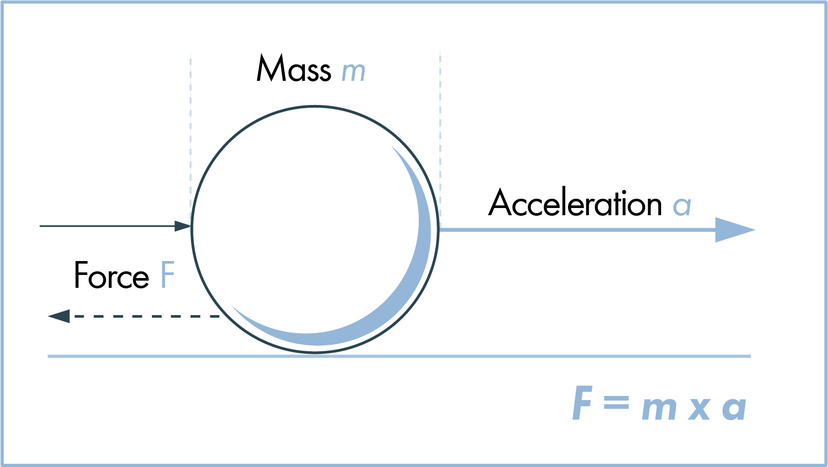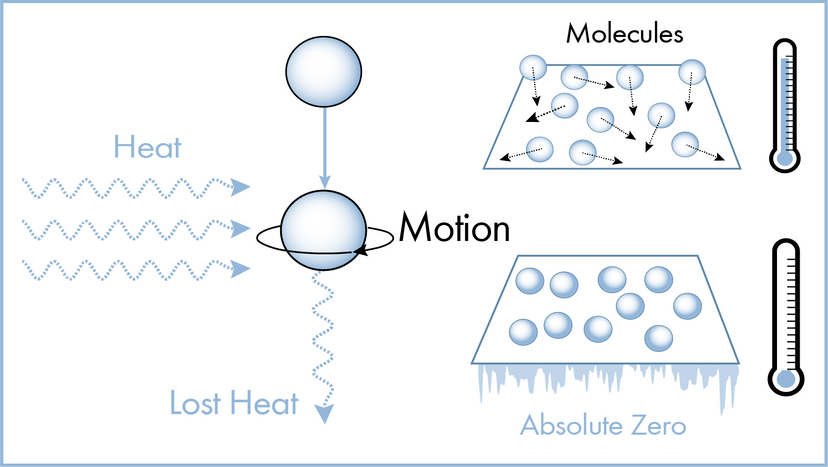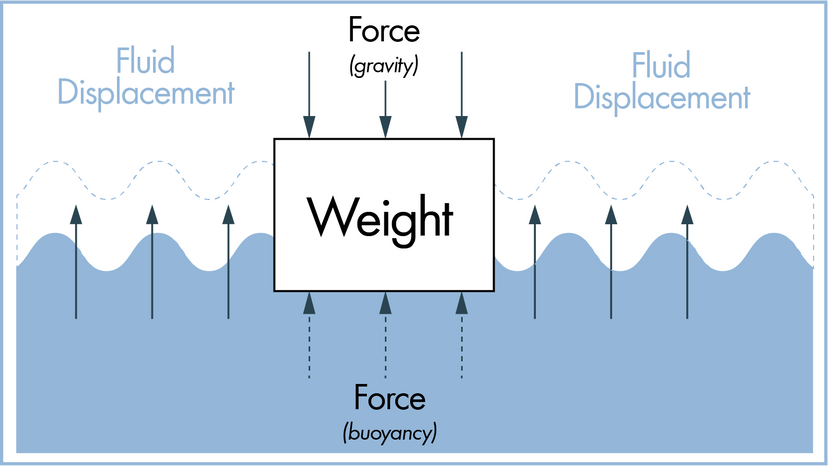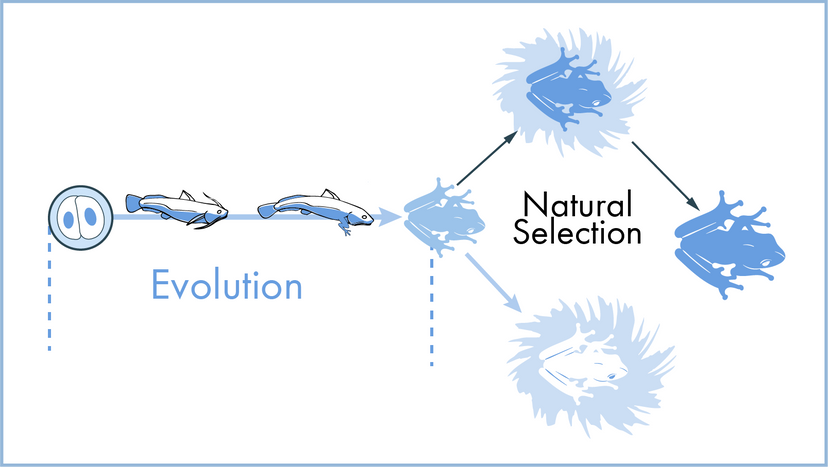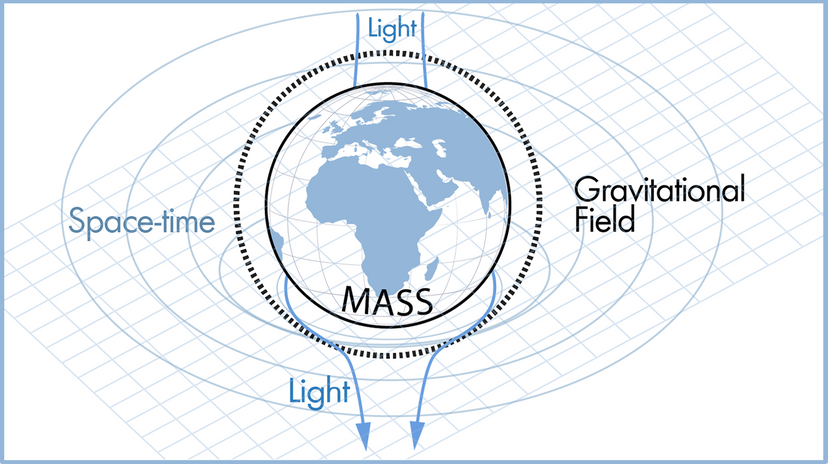
Scientists have many tools available to them when attempting to describe how nature and the universe at large work. Often they reach for laws and theories first. What's the difference? A scientific law can often be reduced to a mathematical statement, such as E = mc²; it's a specific statement based on empirical data, and its truth is generally confined to a certain set of conditions. For example, in the case of E = mc², c refers to the speed of light in a vacuum.
A scientific theory often seeks to synthesize a body of evidence or observations of particular phenomena. It's generally — though by no means always — a grander, testable statement about how nature operates. You can't necessarily reduce a scientific theory to a pithy statement or equation, but it does represent something fundamental about how nature works.
Advertisement
Both laws and theories depend on basic elements of the scientific method, such as generating a hypothesis, testing that premise, finding (or not finding) empirical evidence and coming up with conclusions. Eventually, other scientists must be able to replicate the results if the experiment is destined to become the basis for a widely accepted law or theory.
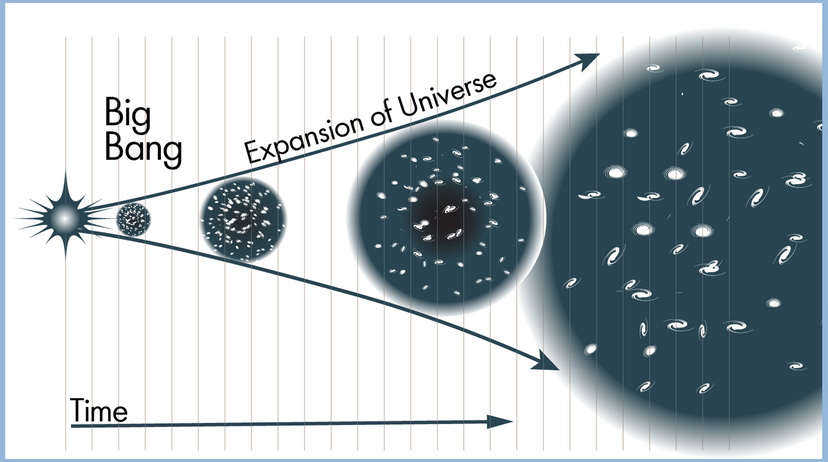
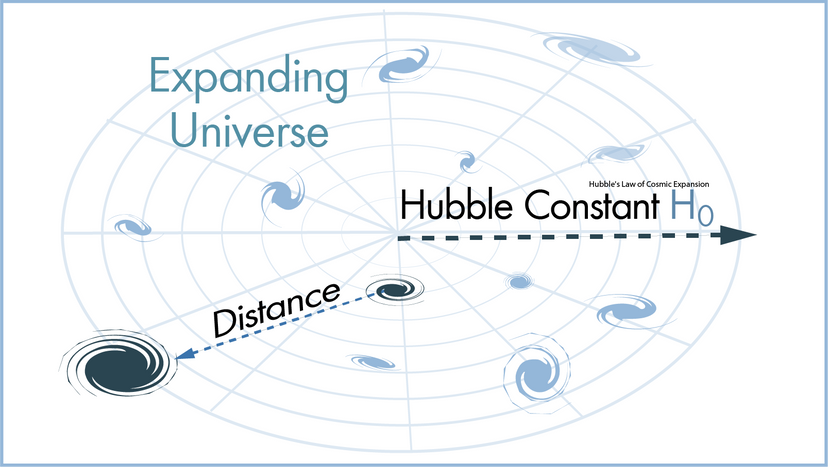
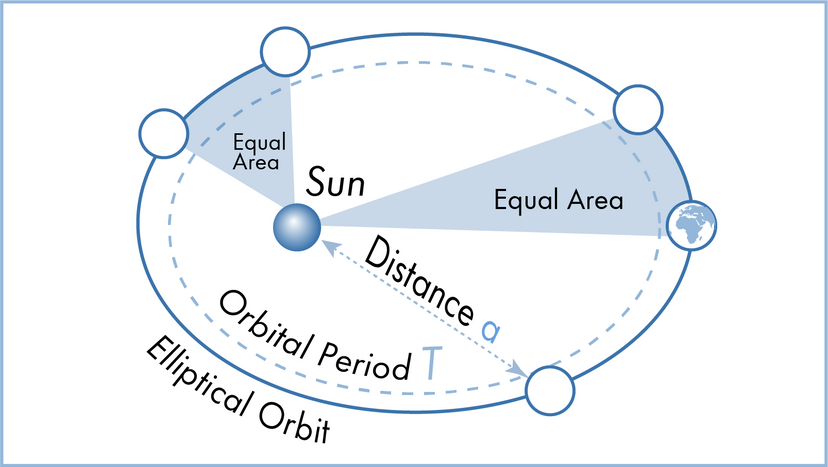
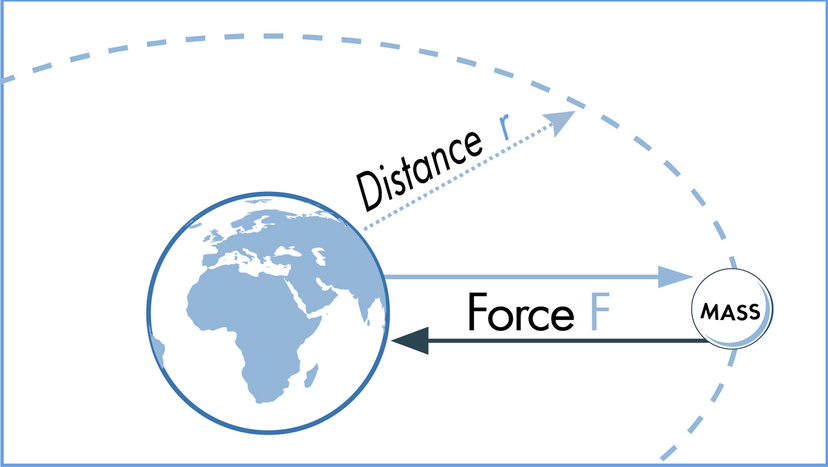
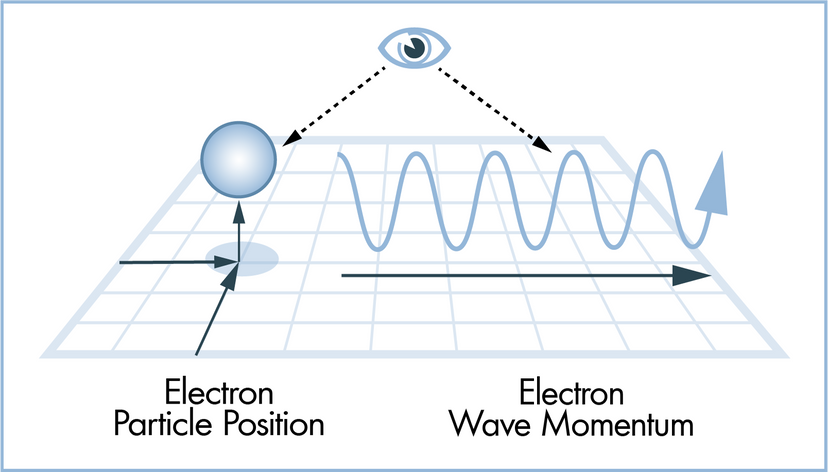
In this article, we'll look at 10 scientific laws and theories that you might want to brush up on, even if you don't find yourself, say, operating a scanning electron microscope all that frequently. We'll start off with a bang and move on to the basic laws of the universe, before hitting evolution. Finally, we'll tackle some headier material, delving into the realm of quantum physics.