Time Intervals
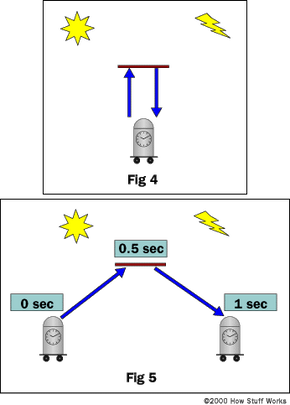
Using the Lorentz Transform, let's put numbers to this example. Let's say the clock in Fig 5 is moving to the right at 90% of the speed of light. You, standing still, would measure the time of that clock as it rolled by to be 2.29-seconds. It is important to note that anyone in motion with the clock in Fig 5 would only measure 1-second, because it would be no different than him standing beside the clock in Fig 4. Hence, the rider aged by 1 second but you aged by 2.29 seconds. This is a very important concept. If we look closely at the clocks, we find that they do not really measure what we think they do. Clocks record the interval between two spatial events. This interval may differ depending on what coordinate system the clock is in (ie. what frame of reference). If the speed of light is held constant (has the same measured value regardless of frame of reference), time is no longer "just" a tool to measure the procession of space. It is a property that is required for the defining and existence of the event. Remember from earlier, any occurrence is an event of space and time (hence, the Space-Time Continuum).
[Note: If the reader decides to learn more about time dilation, it is absolutely imperative that strong emphasis be put on "proper time". This concept is not discussed in this article, but "proper time" is the foundation of the frame geometry of SR. This topic is clearly derived and discussed in the book Spacetime Physics by Taylor and Wheeler.]
Advertisement
The Unification of Energy and Mass
Undoubtedly the most famous equation ever written is E=mc². This equation says that energy is equal to the rest mass of the object times the speed of light squared (c is universally accepted as the speed of light). What is this equation actually telling us? Mathematically, since the speed of light is constant, an increase or decrease in the system's rest mass is proportional to an increase or decrease in the system's energy. If this relationship is then combined with the law of conservation of energy and the law of conservation of mass, an equivalence can be formed. This equivalence results in one law for the conservation of energy and mass. Let's now take a look at a couple examples of this relationship...