Mathematician, physicist, religious philosopher and wordsmith: By any standard, Blaise Pascal exemplified the term Renaissance man.
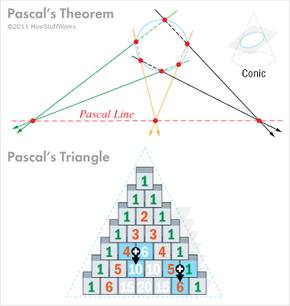
Born on June 19, 1623, in Clermont-Ferrand, France, Pascal established himself in his early teens as a self-taught mathematical prodigy [source: Britannica; "Prodigy"]. At the tender age of 16, he dreamed up Pascal's theorem. According to the theorem, if you draw any hexagon inside any conic section (the curve that occurs when a plane intersects a cone) and then extend the lines of opposite sides, they will meet in three points lying on the same line.
Advertisement
Switching gears, Pascal built one of the first digital calculators in 1642 to aid his father, a mathematician and tax collector, humbly dubbing it the pascaline. The pascaline used gears and pins to perform integer addition. Through a few simple mathematical tricks, a person could also use it to subtract, multiply and divide. Different versions could handle five-, six- and eight-digit numbers. The real trick, though, lay in tackling the nondecimal French monetary denominations, in which 20 sols equaled a livre and 12 deniers made a sol.
As a spinoff of his work on perpetual motion, which he explored in his efforts to improve the pascaline, Pascal also invented the core technology of the roulette machine [source: MIT].
Grade-schoolers still learn Pascal's triangle, a three-sided arrangement of integers such that every number equals the sum of two diagonal numbers above it, as the accompanying illustration demonstrates. Pascal didn't invent the configuration (Chinese and Persian mathematicians used it more than 500 years earlier). However, he found novel uses for it, including calculating probabilities.
In 1654, Pascal, now a worldly 31, brought his knack for formalization and analysis to bear once again as he worked with Pierre de Fermat to establish the calculus of probabilities. While corresponding to solve a gambling puzzle, the two men hit upon the idea of equally probable outcomes, a fundamental concept that had eluded other analysts. A coin flip landing heads or tails, or a single die roll coming up any number from 1-6, are examples of equally probable outcomes. Pascal codified their findings into a general rule for calculating probability, using his handy triangle to simplify the calculations [source: Fermat and Pascal].
Like any Renaissance man worth his salt, Pascal's talents weren't limited to one subject area. Up next, we'll see how his contributions to physics, metaphysics and letters also would reverberate for years to come.
Advertisement