If you have ever looked at the end of a crane, or if you have ever used an engine hoist or a come-along, or if you have ever looked at the rigging on a sailboat, then you have seen a block and tackle at work. A block and tackle is an arrangement of rope and pulleys that allows you to trade force for distance. In this edition of How Stuff Works we will look at how a block and tackle works, and also examine several other force-multiplying devices!
Understanding the Block and Tackle
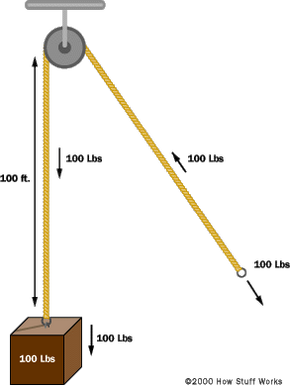
Imagine that you have the arrangement of a 100 pound (45.4 kilogram) weight suspended from a rope, as shown here.
Advertisement
In this figure, if you are going to suspend the weight in the air then you have to apply an upward force of 100 pounds to the rope. If the rope is 100 feet (30.5 meters) long and you want to lift the weight up 100 feet, you have to pull in 100 feet of rope to do it. This is simple and obvious.
Now imagine that you add a pulley to the mix.
Does this change anything? Not really. The only thing that changes is the direction of the force you have to apply to lift the weight. You still have to apply 100 pounds of force to keep the weight suspended, and you still have to reel in 100 feet of rope in order to lift the weight 100 feet.
The following figure shows the arrangement after adding a second pulley:
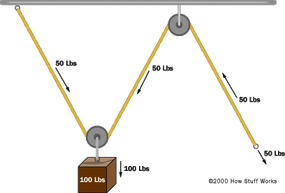
This arrangement actually does change things in an important way. You can see that the weight is now suspended by two pulleys rather than one. That means the weight is split equally between the two pulleys, so each one holds only half the weight, or 50 pounds (22.7 kilograms). That means that if you want to hold the weight suspended in the air, you only have to apply 50 pounds of force (the ceiling exerts the other 50 pounds of force on the other end of the rope). If you want to lift the weight 100 feet higher, then you have to reel in twice as much rope 0- 200 feet of rope must be pulled in. This demonstrates a force-distance tradeoff. The force has been cut in half but the distance the rope must be pulled has doubled.
The following diagram adds a third and fourth pulley to the arrangement:
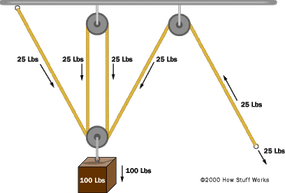
In this diagram, the pulley attached to the weight actually consists of two separate pulleys on the same shaft, as shown on the right. This arrangement cuts the force in half and doubles the distance again. To hold the weight in the air you must apply only 25 pounds of force, but to lift the weight 100 feet higher in the air you must now reel in 400 feet of rope.
A block and tackle can contain as many pulleys as you like, although at some point the amount of friction in the pulley shafts begins to become a significant source of resistance.
Advertisement