Key Takeaways
- Carbon-14 dating works by comparing the ratio of carbon-12 to carbon-14 in a sample to that in a living organism, allowing for the determination of the age of formerly living things fairly precisely.
- The half-life of carbon-14 is 5,700 years, making it reliable for dating organic matter up to about 60,000 years old, with a formula provided to calculate the conventional radiocarbon age (CRA) of a given sample.
- While carbon-14 is commonly used for dating, the principle applies to other isotopes as well, such as potassium-40 and uranium-235, but the accuracy of radioisotope dating may be compromised for anything that dies after the 1940s due to changes in carbon ratios from nuclear activities and fossil fuel burning.
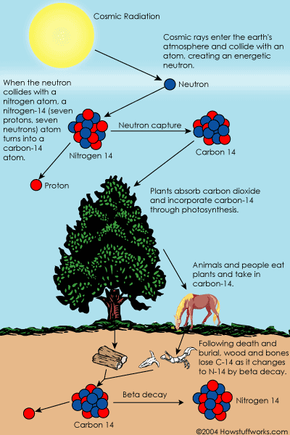
You probably have seen or read news stories about fascinating ancient artifacts. At an archaeological dig, someone unearths a piece of wooden tool and finds it to be 5,000 years old. An archaeologist finds a child mummy high in the Andes and says the child lived more than 2,000 years ago. How do scientists know how old an object or human remains are? What methods do they use and how do these methods work?
Advertisement
Radiocarbon dating, or carbon dating for short, is a way of determining the age of certain archeological artifacts of a biological origin up to about 50,000 years old. It is used in dating things such as bone, cloth, wood and plant fibers that human activities created in the relatively recent past.
Advertisement