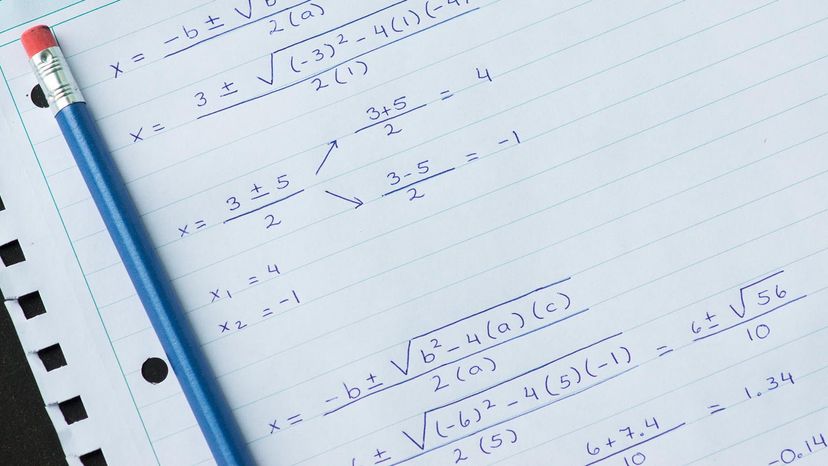Understanding Interval Notation in Mathematics

Whether you're having trouble with empty or unbounded intervals, we have you covered. Kryssia Campos / Getty Images

Mathematicians use something called interval notation to convey information about a range of values in a way that's clear and easy to understand. This form of writing is necessary because intervals are common concepts in calculus, algebra and statistics.

By noting an interval according to a method that's universally understood, mathematicians and students are able to accurately describe and analyze these value ranges.

What's an Interval?

Mathematics defines an interval as a set of real numbers lying between two endpoints on the number line (the endpoints may be included or excluded in the set). Mathematicians commonly express these number sets using interval notation.

The number line is a fundamental tool for visualizing intervals. It helps illustrate how open, closed and half-open intervals differ.

For example, on a number line, a closed interval [a,b] would show both a and b with solid dots, indicating their inclusion in the interval. In this case, values within the interval span would be greater than or equal to a and less than or equal to b.

3 Main Types of Intervals

There are three main types of intervals, each one useful in a different mathematical context.

Open intervals: An open interval, expressed as (a,b), includes all real numbers between a and b, excluding the endpoints themselves. Open interval notation uses parentheses to denote that a and b are not part of the interval.
Closed intervals: Represented by [a,b], closed intervals include both endpoints. Closed interval notation implies that every value between and including a and b is part of the interval. Sometimes, closed intervals coincide on the number line, especially when they share common endpoints.
Half-open intervals: These intervals, also known as half-closed intervals, include one endpoint but not the other. A half-open interval can be either [a,b) or (a,b], where the corresponding square bracket includes the endpoint and the parenthesis excludes the other.

Specific Scenarios in Interval Notation

Beyond the three main types of intervals, there are unique situations that mathematicians need to communicate via interval notation. Here are some examples:

Bounded intervals: These intervals have both endpoints finite, such as [a,b]. A bounded interval is contained entirely within a specific range on the number line. It differs from a closed interval in that a bounded interval uses real numbers, while a closed interval may use complex numbers.
Unbounded intervals: These can be either open or closed at one end while extending infinitely in one direction. For example, (a,∞) and [a,∞) are intervals that start from a and continue indefinitely to the right.

Degenerate interval: A degenerate or trivial interval is where the lower and upper bounds are the same, such as [a,a]. It contains only one element, a, and is both open and closed in nature.
Empty intervals: An empty interval, represented by the empty set symbol ∅, contains no elements. It represents a set with no values and you can, therefore, consider it to be an interval with no span.

Special Concepts

Interval span: Interval span is an important concept to be familiar with when you're discussing interval notation. It refers to the distance between the lower and upper bounds of an interval. With closed intervals, the smallest closed interval containing all its elements will have the smallest possible span.
Finite intervals: Finite intervals have finite endpoints, while infinite intervals have at least one endpoint extending to infinity. Both types can be either bounded or unbounded depending on whether they have limits on both ends.
Disjoint intervals: Mathematicians call two or more intervals disjoint when they have no common points.
Overlapping intervals: On the other hand, if two or more intervals overlap and share at least one point, then mathematicians call them overlapping intervals.

In some contexts, there might be just one interval that satisfies certain conditions, making this unique interval the only interval a mathematician can consider when working on a specific problem or solution as part of a mathematical analysis.

5 Practical Applications of Interval Notation

Modern texts increasingly favor clear mathematical definitions to avoid ambiguity, and interval notation provides a fundamental form of mathematical communication in response to this.

People across multiple fields use this form of notation to denote and analyze the range of functions, sequences or series, from the basics of open and closed intervals to the more intricate concepts. Here are some of the areas in which interval notation has a practical use.

1. Calculus

In calculus, interval notation is crucial for defining the domains and ranges of functions. It helps in specifying intervals where functions are continuous or differentiable.

When discussing integration, you can use interval notation to define the limits of integration, indicating the specific region under the curve you're evaluating.

2. Computer Science

You might use interval notation in algorithm design and analysis to describe the range of inputs for which an algorithm is effective or to specify the bounds within which data can vary.

3. Economics

In economic models, you can use interval notation to define ranges of prices, interest rates or other economic variables within which you're observing or expecting certain behaviors or phenomena.

4. Engineering and Physics

In these fields, interval notation helps you specify the range of permissible values for measurements and variables. For example, you might use it to describe the range of temperatures over which a machine operates efficiently or the span of frequencies in signal processing where a filter is effective.

5. Statistics and Probability

You might use interval notation in statistics to define confidence intervals, which are estimates that likely contain a population parameter within a specified range. It also appears in probability to specify ranges of values for random variables.

We created this article in conjunction with AI technology, then made sure it was fact-checked and edited by a HowStuffWorks editor.