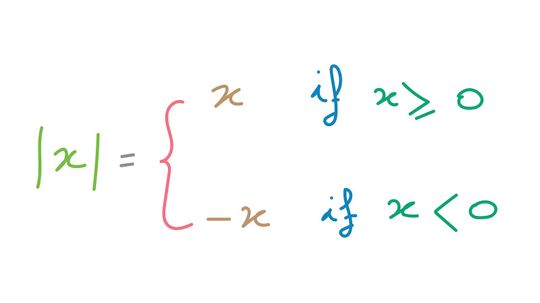Math Concepts
Math is often called the universal language because no matter where you're from, a better understanding of math means a better understanding of the world around you. Learn about math concepts such as addition, subtraction, fractions, ratios and more.
Brown Noise vs. White Noise: Which Is Best for Quality Sleep?

Can a sound wave kill you?

Can two cans and a string really be used to talk over a distance?

7 Types of Alcohol for Drinking, Cleaning and More

Understanding the Empirical Formula in Chemistry

The Most Expensive Metal in the World Isn't Gold or Platinum

How Electricity Works

How Faraday Cages Work

How Gasoline Works

What Does Mummification Have to Do With Gene Hackman?

What do bugs have to do with forensic science?

5 Things You Didn't Know About Autopsies

How Alchemy Paved the Way for Chemistry

How did Nikola Tesla change the way we use energy?

Time May Not Exist, Say Some Physicists and Philosophers

Why Does Ice Stick to Your Fingers?
What if I forgot to remove a piercing before an MRI?

A Kid-friendly Introduction to Magnets and Magnetism

Tonnes vs. Tons: Metric vs. Imperial Measurements Strike Again

The Most Expensive Liquid Is 26,000x the Price of Human Blood

5 Hugely Fun Facts About Mass (Not Weight)

The Demon Core: A Tale of Atomic Ambition and Tragic Fate

Half-Life Formula: Components and Applications

Could an 'X17 Particle' Hint at a Fifth Force in the Universe?

Why Are School Buses Yellow?

HowStuffWorks: How To Draw An Impossible Shape
What Are the Colors in the Visible Spectrum?
Learn More
Mathematics is filled with complex challenges, but the hardest math problem in the world isn’t just a difficult question on a school test: It’s one that defies centuries of logic, calculation, and creativity.
Different problems require different kinds of information, and understanding the types of data is the first step to choosing the right analysis techniques.
Two congruent angles are simply pairs of angles with equal measures. You can find congruent angles examples in hundreds of everyday objects.
By Mitch Ryan
Advertisement
Adjacent angles are one of the earliest and most important concepts to learn in basic geometry, as they have applications in further subjects like trigonometry, physics, and engineering. Effective students of geometry should be able to identify adjacent angles on sight and calculate them to a great degree of accuracy without a protractor.
By Talon Homer
When pursuing an education in mathematics and algebra, one of the earliest and most important concepts to understand is the associative property, also known as the associative law.
By Talon Homer
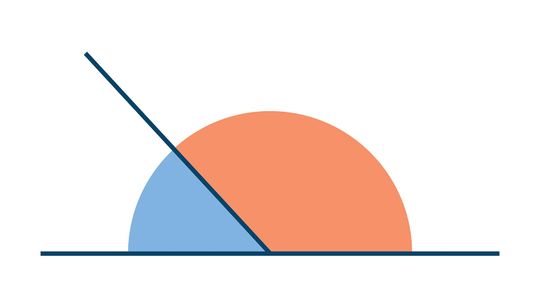
In the subjects of geometry and trigonometry, a linear pair of angles is any two adjacent angles formed together to add up to 180°, or π (pi) radians.
By Talon Homer
With its three sides and three angles, the triangle is one of the most basic shapes in geometry. This means calculating the area of a triangle is a fundamental skill in geometry, with multiple formulas available depending on the type of triangle and the given data.
By Marie Look
Advertisement
In your study of math, you will likely come across the concept of factors at a certain point. While this can be daunting if you've never encountered it before, it won't take long before you're able to determine all the factors of a particular number.
By Zach Taras
Integers are natural numbers (or whole numbers) that stem from the Latin word meaning "intact." In other words, any two integers will be rational numbers. A rational number is a value without fractional part or decimal remainders.
By Mitch Ryan
A rectangular prism is a three-dimensional cuboid figure. In the same way that a triangular prism brings three connected lines to life in the real world, a rectangular prism takes the length and width of two-dimensional rectangles to the next level by adding height into the equation.
By Mitch Ryan
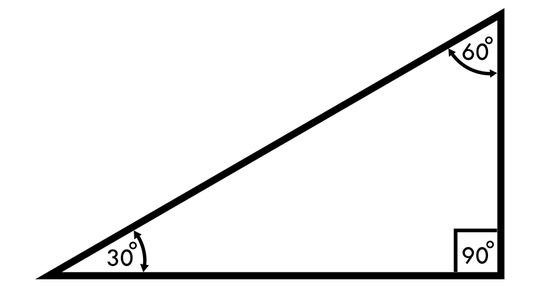
Anyone who's ever faced mind-numbing trigonometry problems and practice questions will be familiar with the Pythagorean Theorem and its square root principles in the 30-60-90 triangle. This special triangle has several short-cut rules to help new mathematicians find interior angles and linear lengths quickly.
By Mitch Ryan
Advertisement
In algebra and calculus, a polynomial function is used to chart out graphs and waves with much more complexity than a simple linear factor. Polynomial division is sometimes required to factor them, and cut them up into chunks that we humans can better understand.
By Talon Homer
Arcs are an important aspect of geometry, physics, trigonometry and design work. However, curved lines are much more difficult to measure than straight lines, which is why it's important to familiarize yourself with the arc length formula.
By Talon Homer
The interquartile range (IQR) is a statistical measure of the middle values of a sample data set that is separated into four equal parts. This middle-value grouping can provide a median range between the upper half and lower half of the data you've collected, allowing you to ignore extreme values.
By Mitch Ryan
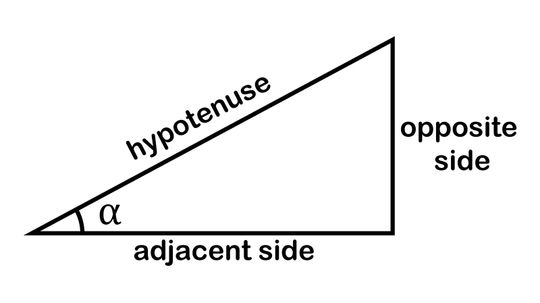
The mnemonic device SOHCAHTOA helps budding mathematicians remember the trigonometric functions sine (sin), cosine (cos) and tangent (tan), which they need to solve for triangles' missing sides and angles.
By Marie Look
Advertisement
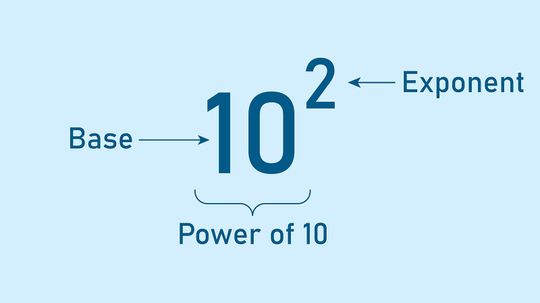
When you're dealing with exponents, numbers can get very big (or very small) very quickly. Therefore, it's helpful to have some short cuts.
By Zach Taras
Absolute value is a mathematical concept often used in conjunction with a number line or graph to represent the relative value from zero (modulus). To illustrate this idea in a different way, the absolute value of a number can be closely related to distance in the physical world.
By Mitch Ryan
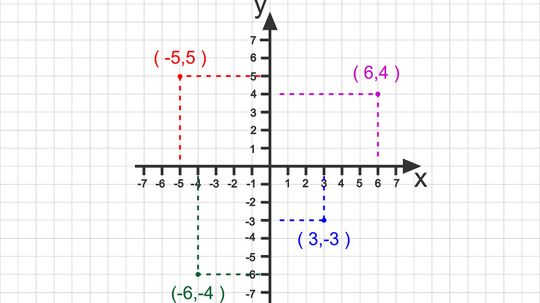
A coordinate plane is a mathematical, two-dimensional plane formed by two number lines. A horizontal number line and a vertical number line intersect to form two axes (plural for axis), and a grid system comprised of four quadrants.
By Mitch Ryan
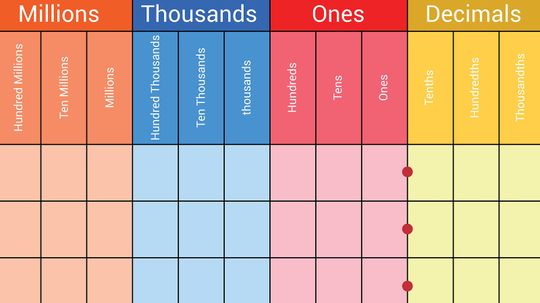
The concept of place values is fundamental to mathematics and the number system, particularly when you're dealing with whole numbers and decimal numbers. A place value chart is an essential tool that can help students visualize the position of each digit in a number and understand its actual value within the context of the number.
By Marie Look
Advertisement
You've probably seen supplementary angles examples in your everyday life without knowing it. Whether you pass a leaning sign on a flat highway or walk by a shed with a lean-to roof - whenever two angles combine to form a straight, linear pair, there they are.
By Mitch Ryan
Mathematicians use something called interval notation to convey information about a range of values in a way that's clear and easy to understand. This form of writing is necessary because intervals are common concepts in calculus, algebra and statistics.
By Marie Look
Fundamental trigonometric identities, aka trig identities or trigo identities, are equations involving trigonometric functions that hold true for any value you substitute into their variables.
By Marie Look
Algebra is the branch of mathematics that focuses on formulas, and one of its key concepts is the representation of linear equations, which describe straight lines.
By Marie Look
Advertisement
Whether you're studying up for a math test, helping your child with homework or just trying to brush up before trivia night, learning the basic ins and outs of polygons will serve you well.
By Mitch Ryan
A rhombus is a parallelogram shape with two pairs of parallel sides and four equal sides. These four sides of equal length also define the rhombus as an equilateral quadrilateral. Etymologically, the name of this shape stems from the Greek word "rhombos," which roughly translates to "spinning top."
By Mitch Ryan