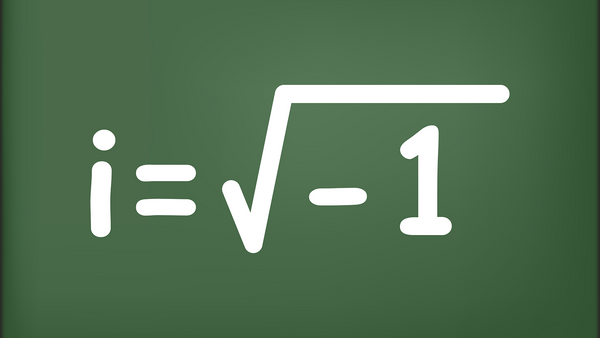What Is the Real Number System?

Math is pretty confusing — at least to people who don't understand it. Which is a lot of us.

The thing about math is you have to learn terms to understand what numbers are, what kinds of numbers are out there and the characteristics of each type. Numbers are just mathematical symbols that we use to count and measure. But not all numbers are created equal.

For instance, take the concept of the "real number system." If numbers can be real, are there also fake numbers? Well, there are real numbers and imaginary numbers. But what does that mean?

Real Numbers Are All the Numbers

Real numbers are basically all the numbers you could think of if somebody told you to think of a number. Real numbers derive from the concept of the number line: the positive numbers sitting to the right of zero, and the negative numbers sitting to the left of zero. Any number that you can plot on this real line is a real number. The numbers 27, -198.3, 0, 32/9 and 5 billion are all real numbers.

Strangely enough, you can also plot numbers such as √2 (the square root of 2, the value of which is 1.14142...) and the decimal equivalent of π (3.1415...), even though they are nonterminating decimal numbers. So, even though the number after the decimal never ends, they still have a place on the number line.

Real numbers include natural numbers, whole numbers, integers, rational numbers, irrational numbers and real numbers.

Natural Numbers

Natural numbers, also known as counting numbers, begin at 1 and go on indefinitely. These positive numbers sit on the right of 0 on the number line. Any one natural number you pick is also a positive integer.

In mathematical notation, the following represents counting numbers: N = {1, 2, 3, 4, 5, 6, ...}.

Whole Numbers

Whole numbers encompass natural numbers as well as 0. In mathematical notation, whole numbers are: W = {0, 1, 2, 3, 4, 5, ...}.

Integers

Integers include whole numbers (0 and natural numbers) as well as numbers with a negative value. The following represents integers: ℤ = {..., -3, -2, -1, 0, 1, 2, 3, ...}. Integers do not include fractions, decimals or fractional parts. They are discrete values.

Rational and Irrational Numbers

Numbers are also either rational or irrational. You can write a rational number as a fraction, which includes whole numbers, all of which you can write as a fraction: 3/8, 5/1, 9/10, etc.

Decimals can fall under the rational category as well — they're just numbers that have either terminating or repeating decimals. So, 8.372 is a terminating decimal and 5.2222222... is a repeating decimal. These are rational numbers, which are also real numbers.

An irrational number is a real number that you cannot express as a simple fraction or ratio of two integers. Instead, rational numbers have non-repeating, non-terminating decimal expansion, such as π (3.14159265...) and √2 (1.41421356...). These decimal expansions go on forever without a repeating pattern.

Absolute Value

The absolute value of a number is a mathematical function that returns the non-negative (aka positive) value of a real number without considering its sign (positive or negative).

For example, if x = 7, then |x| = 7. And if x = -7, then |x| = 7.

It essentially measures the distance of a number from zero on the number line.

Imaginary Numbers

In contrast, an imaginary number is the value of the square root of a negative number. You may remember this special little math rule, but there is no number that, when squared, will produce a negative number.

But that doesn't stop mathematicians from doing it, as long as they admit the result is imaginary. (Infinity is also an imaginary number.)

This article was updated in conjunction with AI technology, then fact-checked and edited by a HowStuffWorks editor.