How Electricity Works

Electrical Circuits

When you load a battery into an electronic device, you're not simply unleashing the electricity and sending it to do a task. Negatively charged electrons wish to travel to the positive portion of the battery -- and if they have to rev up your personal electric shaver along the way to get there, they'll do it. On a very simple level, it's much like water flowing down a stream and being forced to turn a water wheel to get from point A to point B.

Whether you are using a battery, a fuel cell or a solar cell to produce electricity, three things are always the same:

The source of electricity must have two terminals: a positive terminal and a negative terminal.
The source of electricity (whether it is a generator, battery or something else) will want to push electrons out of its negative terminal at a certain voltage. For example, one AA battery typically wants to push electrons out at 1.5 volts.
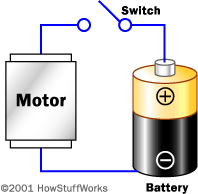
The electrons will need to flow from the negative terminal to the positive terminal through a copper wire or some other conductor. When there is a path that goes from the negative to the positive terminal, you have a circuit, and electrons can flow through the wire.

You can attach any type of load, such as a light bulb or motor, in the middle of the circuit. The source of electricity will power the load, and the load will perform whatever task it's designed to carry out, from spinning a shaft to generating light.

Electrical circuits can get quite complex, but basically you always have the source of electricity (such as a battery), a load and two wires to carry electricity between the two. Electrons move from the source, through the load and back to the source.

Moving electrons have energy. As the electrons move from one point to another, they can do work. In an incandescent light bulb, for example, the energy of the electrons is used to create heat, and the heat in turn creates light. In an electric motor, the energy in the electrons creates a magnetic field, and this field can interact with other magnets (through magnetic attraction and repulsion) to create motion. Because motors are so important to everyday activities and because they are, in essence, a generator working in reverse, we'll examine them more closely in the next section.