The previous section on UV coatings discusses the problem of UV radiation. While the effects of UV radiation are a general concern, other health considerations are more specific. For example, if you have very sensitive eyes, you may wish to use sunglasses that filter a larger portion of the visible light spectrum. Some sunglasses offer protection from infrared radiation as well as UV.
Sunglasses can also be tremendously useful as safety devices. By reducing glare, they allow you to be more visually aware of your surroundings. You may have noticed that most highway patrol officers wear sunglasses. Their sunglasses increase their ability to focus on objects, such as your car speeding by at 75 mph (121 kph), without having to squint.
Performance and Perception
Some sunglasses are equipped with specific filters that reduce glare, increase contrast, or even increase your depth perception. This makes them ideal for certain sports, like beach volleyball, or certain professions, like the highway patrol. Also, by filtering out harmful radiation, sunglasses allow you to spend more time engaged in outdoor activities without suffering some of the drawbacks. Serious fishermen love polarized sunglasses because polarized lenses get rid of the glare coming off the water. This makes it much easier to see deeper into the water and spot that elusive school of fish.
Choosing the Perfect Features for You
The key to finding the perfect pair of sunglasses is to pick the right features for your situation. Here are some of the most important features to compare when you buy a pair of sunglasses:
- Lens material - There are several types of lens material. CR-39 is a plastic made from hard resin that meets optical quality standards. Polycarbonate is a synthetic plastic material that has great strength and is very lightweight. These lenses tend to be lighter and are more impact-resistant. Glass lenses are heavier but are much more resistant to scratches. There are several other materials, such as Oakley's Plutonite plastic, that have been developed by specific manufacturers.
- Lens quality - Optical-quality polycarbonate and glass lenses are free of distortions, such as blemishes or waves, and have evenly distributed color across each lens. Here's an easy way to tell if the lenses in a pair of sunglasses are of good quality. Find a surface with repeating lines, like a tiled floor. Hold the sunglasses a short distance away from your face and cover one eye. Look through one of the lenses at the lines while moving the sunglasses slowly from left to right and then up and down. The lines should stay straight as you look at them. If they wiggle or waver in any way, then the lenses are not optical quality and will distort your vision. Distortion is extremely common in cheap sunglasses.
- Lens darkness - What you plan to use the sunglasses for determines the darkness of the tint. For outdoor sports such as mountain climbing and snow-skiing, you want a tint that blocks most light. (You can buy sunglasses that block up to 97 percent of light!) For most purposes, like going to the beach or driving, look for a tint that absorbs or blocks 70 percent to 90 percent of light. Tints that offer less than 60-percent blockage are mainly good for fashion since they offer only mild protection.
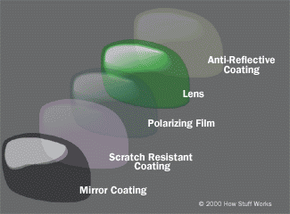
- Special coatings or features - Anti-reflective, waterproof, mirror and scratch-resistant coatings improve the functionality of the sunglasses but also add cost. Many of the more expensive sunglasses use specific technologies including polarization, tinting and anti-reflective coatings to achieve increased clarity, better protection, higher contrast or to block certain types of light.
- Frame and lens design - Normal frames similar to prescription eyeglass frames filter the light coming through the lenses but offer no protection from ambient light, direct light and glare from other angles. Wrap-around frames, larger lenses and special sidereal attachments can keep this extra light from your eyes.
- Frame material - The material used to make the frames is often a huge factor in cost and durability. Most inexpensive sunglasses use simple plastic or wire frames, while name-brand sunglasses by companies like Revo, Maui Jim and Serengeti use high-strength, light-weight composite or metal frames. Also, the better sunglasses usually have features like tension springs that connect the arms to the face instead of just screws.
- Brand recognition - The simple truth is that a brand name does add cost. Just like shoes and suits, people associate certain brands with quality and extravagance. Some companies spend huge amounts of money to advertise a brand and create an identity. That cost is often passed on to the consumer in the product's price. If "brand name" is important to your image, then buying a brand name is important. However, it is possible to find high-quality sunglasses that don't have a brand-name price. Shops like REI often sells store-brand glasses of good quality at a much lower price.
Fashion and image do play a role in sunglass selection. Ever since the 1960s, when FosterGrant ran the "Who's That Behind Those FosterGrants?" ad campaign, sunglasses have continued to increase in popularity. From Jack Nicholson in "Easy Rider" and John Belushi and Dan Akroyd in "The Blues Brothers" to Tom Cruise in, well, anything ("Risky Business," "Top Gun," "Jerry Maguire," "Mission Impossible II"), sunglasses have become a fashion icon. Styles range from conservative to outrageous, and come in every conceivable color.
There is a certain mystique when someone wears sunglasses. It is often said that the eyes are the windows to the soul, so it is no wonder that a device that hides them makes the wearer seem more provocative and mysterious.
For more information on sunglasses and related topics, check out the links on the next page.