Imagine you're a soldier posted on a defensive line. Tomorrow, there will be a great battle. There are two possible outcomes of the battle (victory or defeat), and two possible outcomes for you (surviving or dying). Clearly, your preference is to survive.
If your line is breached, you will die. However, even if the defensive line holds, you may die in battle. It seems that your best option is to run away. But if you do, the ones who stay behind and fight may die. You realize that every other person on the defensive line is thinking this very same thing. So if you decide to stay and cooperate but everyone else flees, you'll certainly die.
Advertisement
This problem has plagued military strategists since the beginning of warfare. That's why there is generally a new condition entered into the equation -- if you flee or defect, you will be shot as a traitor. Therefore, the best chance you have of surviving is to keep your position on the line and fight for victory.
How does this relate to game theory?
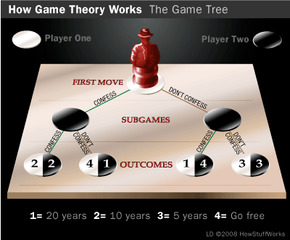
Game theory isn't the study of how to win a game of chess or how to create a role-playing game scenario. Often, game theory doesn't even remotely relate to what you'd commonly consider to be a game.
At its most basic level, game theory is the study of how people, companies or nations (referred to as agents or players) determine strategies in different situations in the face of competing strategies acted out by other agents or players. Game theory assumes that agents make rational decisions at all times. There's some fault in this assumption: What passes for irrational behavior by most of society (a buildup of nuclear weapons, for instance) is considered quite rational by game theory standards.
However, even when game theory analysis produces counterintuitive results, it still yields surprising insights into human nature. For instance, do members of society only cooperate with each other for the sake of material gain, or is there more to it? Would you help someone in need if it hurt you in the long run?
To learn why a rational person must behave selfishly, continue to the next section.