Humans spent the last five and a half millennia inventing over 100 different ways to write down numbers. With due respect to Roman numerals, the world's favorite technique right now is — by a huge margin — the modern decimal system. Its users can express any whole number they like with just 10 little characters: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
However, your computer takes another approach. Laptops, smartphones, and other devices rely on binary code. A mathematical language, binary relays instructions to these high-tech gizmos. It tells your computer how a podcaster's voice sounds, which colors should appear in a YouTube video, and how many letters were used in that email your boss just sent.
Advertisement
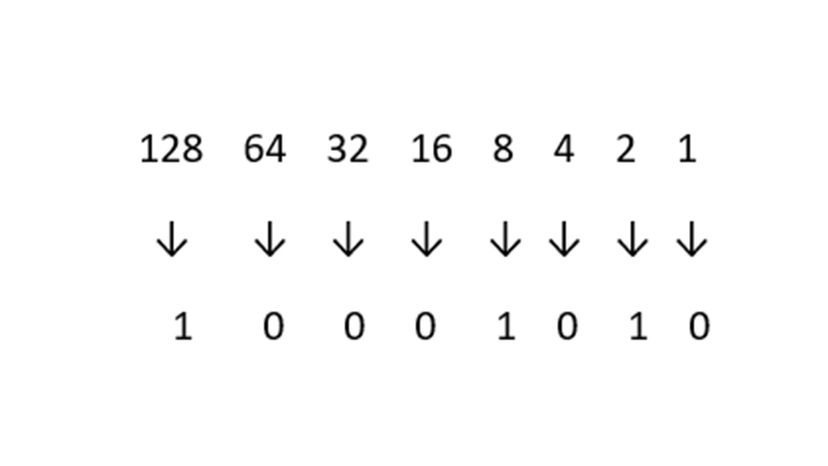
Binary code lives up to its name. Unlike the decimal number system, it uses only two digits, which programmers call "bits." Usually, there's "0" and there's "1." And that's all. Luckily, we'll show you how to convert a binary number into the more familiar decimal system. Then, like a good magician, we'll do the exact opposite, bringing the decimal to binary value.