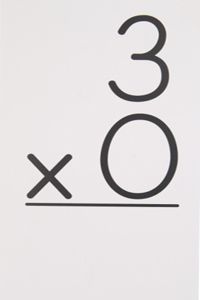Alex the grey parrot was probably bored. He was 27 years old and for 26 of those years, he'd had researchers similar to the ones now testing him ask primitive questions like, "Alex, what color is four?" Typically, he was a whiz at these kinds of tests; he would scan the tray with a variety of objects on it, find the four orange rods and answer, "orange." In fact, in tests of his ability to count to four, he answered correctly 80 percent of the time in this particular study. But today he seemed bored. He'd been doing what the researchers called "balking" for two weeks now: staring at the ceiling, reciting a word over and over and requesting to be put back in his cage.
So one can imagine the surprise among the psychologists conducting the counting experiment with him, when after all this balking, he interjected the word "none." After testing a new hypothesis they generated following Alex's spontaneous use of the "none," the researchers found that their suspicions were correct. Alex was using "none" as a word for "zero," in this case the absence of quantity. He scored better in tests of zero quantity (83.3 percent) than he did for identifying four objects.
Advertisement
The fact that, when asked how many spools were present on the tray when indeed there were zero spools present, a parrot would correctly answer none was described by the researchers as "striking" [source: Pepperberg and Gordon]. After all, it was only a couple thousand years ago that zero made its first appearance among humans. It's been even less time that we've understood zero as a number.
Then again, under certain circumstances, zero isn't a number at all. In some cases, it's the opposite of infinity. In other cases, it's the mathematical equivalent of a bump on a log. In still others, it's the pivot point for all other numbers. And in any case, it is the number that captures the human imagination more than any other. The very existence of this article is evidence of that; you won't find the article How Eighteen Works anywhere on this site. Zero is also the number -- aside, arguably, from 666 -- with the darkest connotations. Cultures across the span of time and space long shunned the concept of zero, equating it with primeval void and chaos, the ingredients for the Christian concept of Hell.
In this article, we'll examine zero as a concept, a number and a key to mathematics. On the next page, we'll look at how humans came across it in the first place.