Before there were global supply chains and trade agreements, convenience was the highest priority when it came to measurement. In most cases, people didn't have access to sophisticated measuring devices, so they relied on body parts, which were easy to carry around and offered somewhat consistent results. For example, the width of a man's thumb is about an inch ("thumb" and "inch" are interchangeable in many languages).
This crude, informal system worked fine for many years, but it began to fall apart as clans grew into tribes and tribes grew into nations. As civilizations expanded, their conflicting systems of measurement created confusion and interfered with commerce. In France, the situation had become particularly chaotic by the time the French Revolution began in 1789. Measures for length, volume and mass differed from one town to the next. Many people believed that the system used in Paris, based on units dating back to Charlemagne, should be imposed on the whole country, but the guilds and nobles fought the effort. With the French government on the verge of financial collapse, King Louis XVI convened the Estates General -- an assembly made up of representatives from the country's various classes -- to levy new taxes. Ultimately, the legislative session proved more fruitful, leading to the formation of the National Assembly, a new constitution and a new way to measure things.
Advertisement
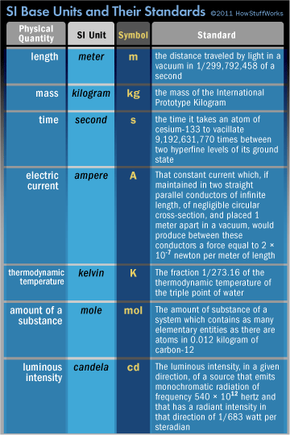
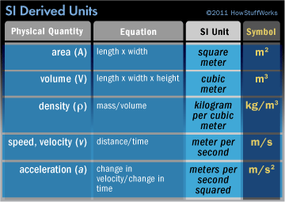
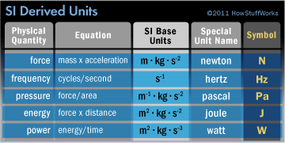
The French called the new system of measurement métrique, a term derived from the word mètre, or meter -- a fundamental measure of length defined as one ten-millionth of a quarter of the Earth's meridian passing through Paris. The developers of this new measuring system believed their work would be an "enterprise whose result should belong someday to the whole world" [source: Nelson]. They were right, of course, for the metric system today has been adopted by almost every country on the planet. The only significant partial holdout is the United States, whose citizens greet meters, liters and kilograms with mild suspicion and, in some cases, bewilderment. What many people don't realize is that the U.S. has been a strong supporter of the metric system since the Civil War and that units of the inch-pound system are defined exclusively in terms of metric measurements.
Before we dive into the minutiae of metric, let's elaborate a bit more on the history of the world's measuring system and how it came to take its modern form, the Système International d'Unités -- the International System of Units, or SI.
Advertisement