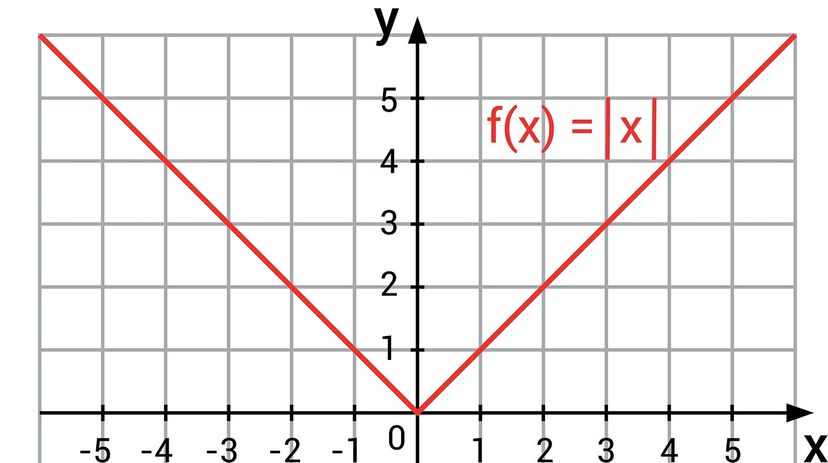
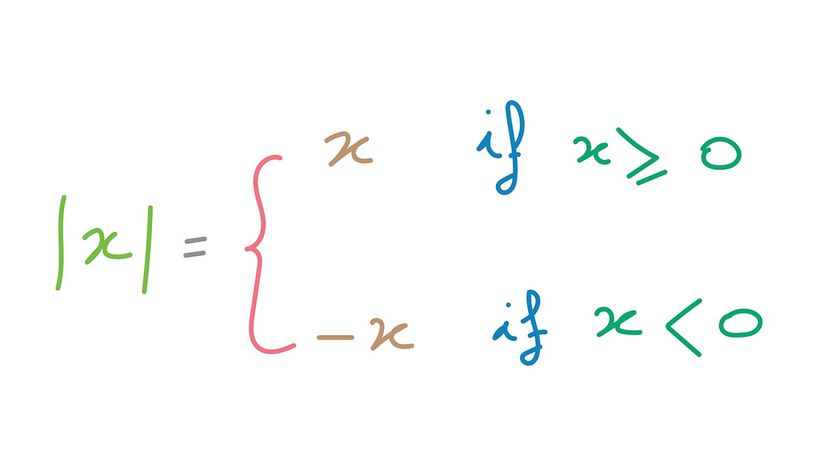How Absolute Value Works in Equations and Graphs

You can figure out the absolute value of x in a couple different ways. We'll explain. Dream01 / Shutterstock

Absolute value is a mathematical concept often used in conjunction with a number line or graph to represent the relative value from zero (modulus). To illustrate this idea in a different way, the absolute value of a number can be closely related to distance in the physical world.

To illustrate this concept, regard your house as the origin point "zero," with steps toward the west as negative numbers, and steps toward the east as positive numbers. Whether you traveled a mile east or a mile west, you are an equal distance away from your home.

Walking west didn't mean you were taking a negative number of steps, and going east isn't equivalent to a positive number of steps. They have the same positive value from the origin point. Therefore, a mile in either direction has the same absolute value.

What Does an Absolute Value Symbol Look Like?

Absolute value symbols are vertical bars on each side of a number. For instance, instead of writing "the absolute value of five," you can simply write |5|.

4 Fundamental Properties of Absolute Values

Now that you understand the general meaning of absolute value from the distance example above, read on to learn how you can use the following four fundamental properties to quickly identify and define a specific instance of this mathematical concept.

1. Non-negativity

An absolute value will always be a positive or non-negative value.

2. Positive-definiteness

In regards to absolute value, positive definiteness means that a number's absolute value is zero only when the number is explicitly denoted as zero |0|.

3. Multiplicativity

The absolute value of the product of two numbers is the same as the product of the absolute values because of what the negative sign becomes in an absolute value. Let's look at the following example.

The absolute value of the product of -3 and 5 is 15:

|-3 x 5| = |-15|

|-15|= 15

The product of |-3| and |5| is also 15:

|-3| x |5| = 3 x 5

3 x 5 = 15

4. Subadditivity

The concepts of subadditivity are typically illustrated in the following expression:

|a + b| ≤ |a| + |b|

This means that the absolute value of the sum of two real numbers is less than or equal to the total of the absolute values of the two numbers. Let's plug in some numbers to see how this plays out in a real example:

Whether a is -2 or 2, |a| is 2. Similarly, whether b is -5 or 5, |b| is 5. Therefore:

|a| + |b| = |2| + |5|

|2| + |5| = 2 + 5

2 + 5 = 7

Now let's look at the other side of that inequality: |a + b|. The expression a + b (before you take the absolute value of the expression) can play out any of the following ways:

-2 + -5 = -7

2 + (-5) = -3

-2 + 5 = 3

2 + 5 = 7

The absolute value of the first and last examples is 7:

|7| = 7

|-7| = 7

The same goes for the second and third examples:

|3| = 3

|-3| = 3

Now, let's go back to the initial inequality: |a + b| ≤ |a| + |b|. No matter what values you plug into a and b, you'll find that the absolute value of the sum (|a + b|) is less than or equal to the sum of the absolute values (|a| + |b|).

Solving Absolute Value Equations

First, separate the absolute value expression from the rest of the equation. Identify whether it is a positive or negative value and how it will affect the corresponding numbers. Solve the unknown and double-check your work by graphing it.

Absolute Value Function Graphs

graph of absolute value function in coordinate system — This is the graphical representation of f(x) = |x|. zizou7 / Shutterstock

In mathematical settings it is always important to proof your work to validate your answer. The graph of the common form of the absolute value function is f(x) = |x|.

This formula can also be expressed as f(x) = x, if x ≥ 0 and -x, if x < 0 (as depicted in the image at the beginning of the article).