
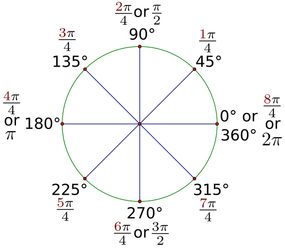
Degrees and radians are fundamental units that help measure angles. A circle comprises 360 degrees, which is equivalent to 2π radians. But if you're wondering how to convert degree to radian, the answer is simpler than you might think.
Advertisement

Degrees and radians are fundamental units that help measure angles. A circle comprises 360 degrees, which is equivalent to 2π radians. But if you're wondering how to convert degree to radian, the answer is simpler than you might think.
Advertisement
To convert degrees into radians, you just need to memorize a few easy steps.
First, take the number of degrees you wish to convert. Multiply the given value of the angle in degrees by π radians/180 degrees (180 degrees = pi radians). By eliminating some redundant units and then simplifying things a bit, you'll have your answer.
Advertisement
Suppose you've got a metal bar that's been bent at a 120 degree angle. How can we express this in terms of radians?
To find out, we'll write our equation in the following formula:
120° x (π radians/180°)
Notice the pair of degree symbols shown above. Those will cancel each other out, ensuring our final answer will be in radians. We are now left with:
120 x (π radians/180)
Do the multiplication and you get 120π/180 radians. But we’re not quite done yet. Now we’ve got to simplify our fraction if possible. We need to identify the highest whole number that can be divided exactly into both the denominator (180) and the non-π portion of the numerator (120). Spoiler alert: In our case, the magic number is 60.
If you actually divide 120π and 180 by 60, you get 2π/3 radians.
So, there we go: the original angle measure (120°) is equal to 2π/3 radians.
To convert radians to degrees is a similar procedure. In the radians formula, in this case, we'd take the starting amount of radians and multiply it by (180°/π).
π/3 radians x (180°/π) = 60 degrees
Conversion formula summarized:
To convert radians to degrees: multiply by 180, divide by π
To convert degrees to radians: multiply by π, divide by 180
Advertisement
Now you might be wondering, how would you go about converting a negative degree into a radian. Well, the method is the same for positive degrees. You'll simply multiply the value of the given angle in degrees by π/180.
For example, to convert -180 degrees into radians the equation is as follows:
Advertisement
Radian = (π/180) x (-180°)
Angle in radian = – π
Advertisement
There's an infamous quote attributed to NBA coach and former player Jason Kidd: "We're going to turn this team around 360 degrees!"
Whoops. Math teachers must've rolled their eyes at that one.
Advertisement
As you might already know, a circle is made up of exactly 360 degrees. If Kidd had made good on his promise, then his team would have turned around all right. The trouble is, the squad wouldn't stop turning until it had "gone full circle" and ended up right back where it started.
Not a recipe for improvement. What Kidd was looking for was to turn his team around 180 degrees and make them winners!
Advertisement
The degree, in this context, is a unit we can use for measuring angles. They're also sometimes referred to as degree of arc, arc degree, or arcdegree. On paper, degrees are represented by the degree symbol, which looks like this: °
So instead of writing "18 degrees," you could simply write "18°."
Advertisement
One of the most important concepts in trigonometry and geometry is the right angle. This is the angle that's formed where two perpendicular lines intersect.
It also represents one-quarter of a full rotation.
Let's say you want to physically turn something. Anything. You've chosen a fixed center point and are trying to maneuver that object around it in a circular motion. If you finish the job and make a complete circle, that's a full rotation. But if you stop the process 25 percent of the way through, that's only one quarter of a full rotation. Which gives you a right angle.
A right angle is equal to 90 degrees (i.e., 25 percent of 360). Here's another way of putting it: A right angle is equal to π/2 radians.
Time-out! What's a radian? And how did π (pi) get mixed up in this?
Advertisement
In the realm of trigonometry and geometry, radians stand as an essential unit for measuring angles. While degrees are a common choice, especially for everyday use, radians offer a more precise and elegant way to work with angles in mathematics, physics, and engineering.
What Is a Radian?
Advertisement
A radian, often denoted as "rad," is a unit of angular measurement that defines the extent of an arc subtended by an angle at the center of a circle. More formally, one radian is defined as the angle subtended at the center of a circle when the arc length is equal to the radius of the circle. This seemingly abstract definition holds the key to understanding radians and their significance.
Relationship Between Radians and Degrees
To grasp the connection between radians and degrees, consider a circle with a radius 'r.' If you were to trace an arc along the circumference of this circle, sweeping out an angle 'θ' at its center, the length of that arc would be 'rθ.' This simple relation forms the basis of the radian formula.
Now, imagine the same circle with a complete counterclockwise revolution, which is equivalent to 360 degrees. In radians, this corresponds to a full circumference, which has an arc length of '2πr.' Hence, 360 degrees is equal to 2π radians.
To put it more succinctly, one radian is approximately 57.3 degrees (or 180/π degrees).
Radians offer a unique advantage when dealing with trigonometric functions, especially when performing calculus and advanced mathematical operations. Trigonometric functions like sine and cosine are most naturally expressed in terms of radians, making calculations more straightforward and elegant.
Consider the sine function, for instance. In radians, the sine of an angle 'θ' can be represented as sin(θ), and the arc length on the unit circle corresponding to this angle is 'θ.' This intuitive relationship simplifies the understanding of these functions and their applications in various scientific and engineering disciplines.
Why Radians Matter
While degrees are well-suited for everyday tasks and basic geometry, radians shine in the world of advanced mathematics and physics. They offer a more precise and intuitive means of measuring angles, especially when dealing with circles, curves, and complex functions. Radians not only streamline calculations but also reveal the profound mathematical connections between angles and circular motion.
Advertisement
Look, we won't deny it. Radians can be a harder concept to visualize than degrees are.
But don't discount the former. Both of these angle-measuring units have their advantages and both degree and radian represent the measure of an angle.
Advertisement
The degree is way more popular. Out in the real world, you're more likely to encounter people who think in terms of degrees as opposed to radians. After all, who would want to be measuring angles in radians in decimal form? So, if you're trying to communicate with a non-mathematician, maybe stick to degrees.
However, the issue with only working with degree measure is that it hinders your ability to apply angles to other functions. Plus, in calculus, radians are great because they lend themselves to much simpler equations. Future A.P. students will want to keep that in mind.
This article was updated in conjunction with AI technology, then fact-checked and edited by a HowStuffWorks editor.
Advertisement
Please copy/paste the following text to properly cite this HowStuffWorks.com article:
Advertisement