What Is the Formula for Velocity?

velocity formula — When you're calculating velocity, you're determining how fast an object moves from its original position, with respect to a frame of reference, and a function of time. That means an object's velocity will be equal to the object's speed and direction of motion. petrroudny43/Shutterstock/HowStuffWorks

Key Takeaways

Speed and velocity are distinct concepts; while speed only considers the magnitude of movement, velocity also takes into account the direction.
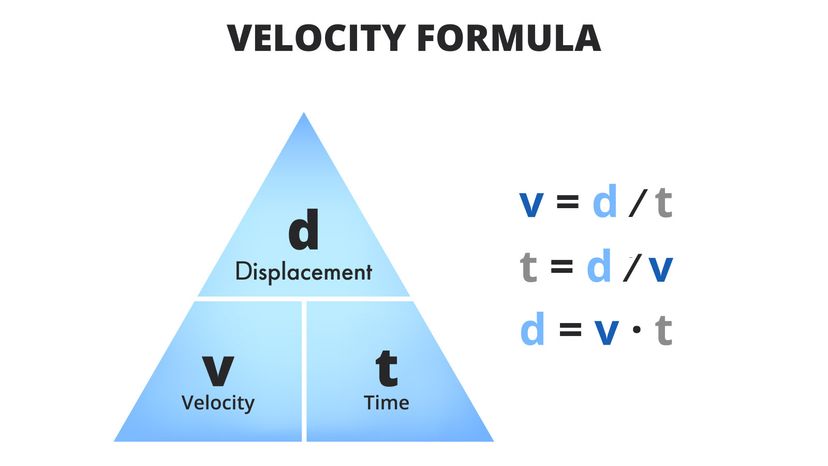
The formula for velocity is given by velocity (v)=displacement (d)time (t)velocity (v)=time (t)displacement (d), where displacement is the distance covered in a specific direction.

Far be it for us to criticize speeding tickets as a public safety tool (and a source of municipal revenue), but maybe law enforcement officials should think about renaming them "velocity tickets."

Allow us to make our case. You see, while the two concepts are related, the words "speed" and "velocity" do not, however, in physics, refer to the same thing.

Velocity, Defined

Speed is the total distance over which an object travels during a particular interval of time.

Velocity adds something else to the conversation. Being what physicists call a "vector quantity," velocity incorporates both magnitude and direction. On the other hand, speed is a "scalar quantity," a phenomenon that deals with magnitude — but not direction.

Michael Richmond, Ph.D., professor at Rochester Institute of Technology's School of Physics and Astronomy, defined velocity as "the rate at which displacement changes with time."

Covering Ground

What, pray tell, is "displacement?" Basically, this marks an object's change in position or the difference between where it physically started and where it ends up.

Note that the change in an object's position is not always equal to the distance it's traveled. That might sound counterintuitive, but bear with us.

Run one lap in a perfect 8-foot (2.4-meter) circle and you will have covered a distance of 8 feet.

However, you will also have circled right back to your original starting point. So that means your displacement will be equal to 0 feet (i.e., 0 meters), even though you traveled a greater distance.

Learning By Example

Time for another hypothetical.

Let's say you're at the gym making small talk. If another patron were to tell you "Gary sprinted 39.3 feet (12 meters) in three seconds today," they'd be giving you his speed, but not his velocity.

To calculate Gary's velocity, we'd need more information.

If our gym buddy said, "Gary sprinted 39.3 feet (12 meters) west in three seconds today," then we'd know about his direction of travel and be off to a good start.

The formula for calculating an object's velocity is as follows:

v = d/t

Here, the letters "v," "d" and "t" respectively denote "velocity," "displacement" and "time." In other words, velocity = displacement divided by time.

When using this formula, it's important to measure displacement in meters and time in seconds. For simplicity's sake, let's assume that old Gary ran to the west in a perfectly straight, 12-meter (32.8-foot) line, so his displacement equals the distance he traveled.

We also know that it took him three seconds to cover the gap between his starting and ending points.

Therefore, when we plug in the numbers, we get this:

v = 12/3

Ergo, westbound Gary had an average velocity of 4 meters per second (13.12 feet per second).

(Phrasing matters here. All we've done is calculate Gary's average velocity; we haven't addressed the subject of instantaneous velocity, a phenomenon that puts its own twist on the formula broken down above.)

Closing Comments

Now ... about those so-called "speeding" tickets. If you've ever received one, the direction in which your vehicle was headed at the time must've been a factor. Consciously or not, it's something both you and the police officer considered.

Know what's worse than driving way too fast? Driving way too fast in an illegal direction. (Consider one-way streets. Or even two-lane roads that force the motorists on one side to travel at a slower pace.)

So yeah, given all we've learned today, we think you could make the case that "speeding tickets" should really be called "velocity tickets." Or something similar. Good night, everybody.