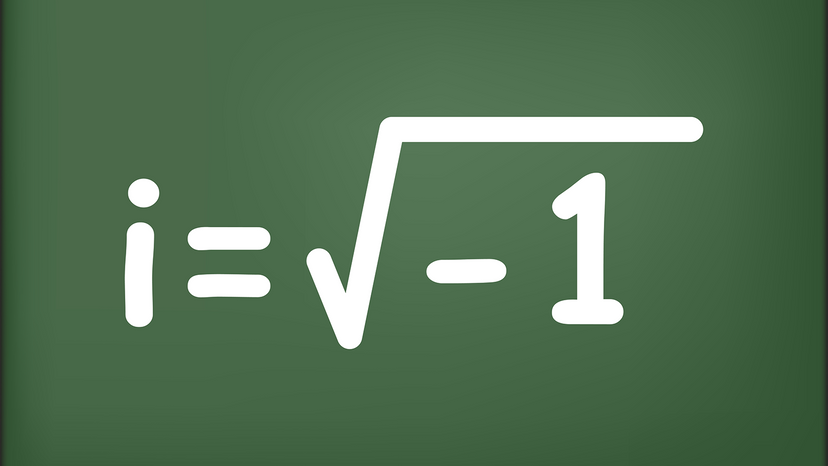
For those of us who aren't mathematically inclined, the notion of imaginary numbers is a bit puzzling. What in the heck does that even mean? Are these made-up numbers? Are they invisible like imaginary friends? Send math help!
Advertisement
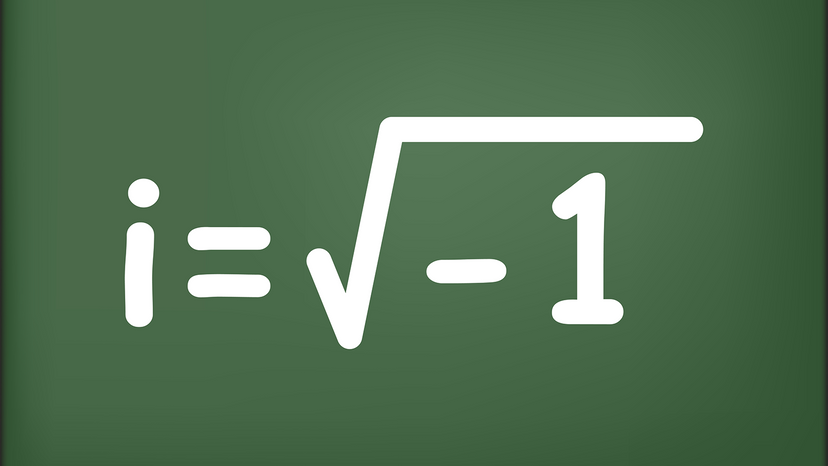
For those of us who aren't mathematically inclined, the notion of imaginary numbers is a bit puzzling. What in the heck does that even mean? Are these made-up numbers? Are they invisible like imaginary friends? Send math help!
Advertisement
An imaginary number — basically, a number that, when squared, results in a negative number — was first established back in the 1400s and 1500s as a way to solve certain bedeviling equations.
While initially thought of as sort of a parlor trick, in the centuries since, imaginary numbers have come to be viewed as a tool for conceptualizing the world in complex ways, and today are useful in fields ranging from electrical engineering to quantum mechanics.
Advertisement
"We invented imaginary numbers for some of the same reasons that we invented negative numbers," explains Cristopher Moore. He's a physicist at the Santa Fe Institute, an independent research institution in New Mexico, and coauthor, with Stephan Mertens, of the 2011 book "The Nature of Computation."
"Start with ordinary arithmetic," Moore continues. "What is two minus seven? If you've never heard of negative numbers, that doesn't make sense. There's no answer. You can't have negative five apples, right? But think of it this way. You could owe me five apples, or five dollars. Once people started doing accounting and bookkeeping, we needed that concept."
Similarly, today we're all familiar with the idea that if we write big checks to pay for things but don't have enough money to cover them, we could have a negative balance in our bank accounts.
Advertisement
Another way to look at negative numbers — and this will come in handy later — is to think of walking around in a city neighborhood, Moore says.
If you make a wrong turn and in the opposite direction from our destination — say, five blocks south, when you should have gone north — you could think of it as walking five negative blocks to the north.
Advertisement
"By inventing negative numbers, it expands your mathematical universe, and enables you to talk about things that were difficult before," Moore says.
Imaginary numbers and complex numbers — that is, numbers that include an imaginary component — are another example of this sort of creative thinking. As Moore explains it: "If I ask you, what is the square root of nine, that's easy, right? The answer is three — though it also could be negative three," since multiplying two negatives results in a positive.
But what is the square root of negative one? Is there a number, when multiplied by itself, that gives you negative one? "At one level, there is no such number," Moore says.
But Renaissance mathematicians came up with a clever way around that problem. "Before we invented negative numbers there was no such number that was two minus seven," Moore continues. "So maybe we should invent a number that is square root of negative one. Let's give it a name. i."
Once they came up with the concept of an imaginary number, mathematicians discovered that they could do some really cool stuff with it. Remember that multiplying a positive by a negative number equals a negative, but multiplying two negatives by one another equals a positive.
But what happens when you start multiplying i times seven, and then times i again? Because i times i is negative one, the answer is negative seven. But if you multiply seven times i times i times i times i, suddenly you get positive seven. "They cancel each other out," Moore notes.
Now think about that. You took an imaginary number, plugged it into an equation multiple times, and ended up with an actual number that you commonly use in the real world.
Advertisement
It wasn't until few hundred years later, in the early 1800s, that mathematicians discovered another way of understanding imaginary numbers: thinking of them as points on a plane, explains Mark Levi. He's a professor and head of the mathematics department at Penn State University and author of the 2012 book "Why Cats Land on Their Feet: And 76 Other Physical Paradoxes and Puzzles."
When we think of numbers as points on a line, and then add a second dimension, "the points on that plane are the imaginary numbers," he says.
Advertisement
Envision a number line. When you think of a negative number, it’s 180 degrees away from the positive numbers on the line. "When you multiply two negative numbers, you add their angles, 180 degrees plus 180 degrees, and you get 360 degrees. That's why it's positive," Levi explains.
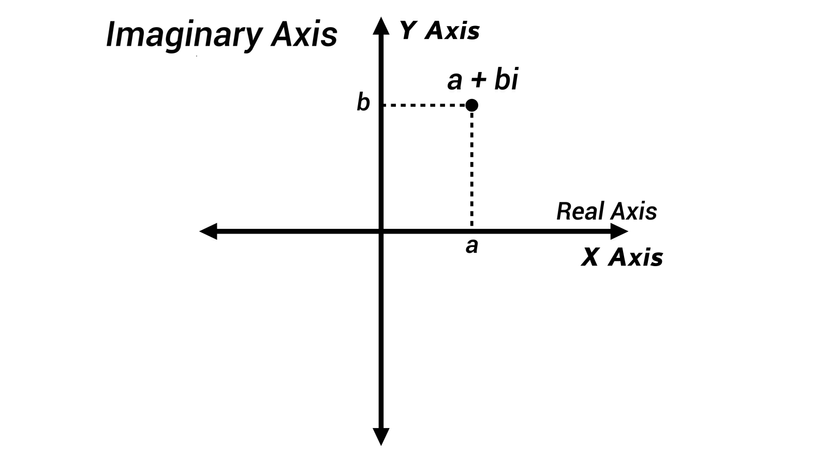
But you can't put the square root of negative one anywhere on the X axis. It just doesn't work. However, if you create a Y axis that's perpendicular to the X, you now have a place to put it.
And while imaginary numbers seem like just a bunch of mathematical razzle-dazzle, they're actually very useful for certain important calculations in the modern technological world, such as calculating the flow of air over an airplane wing, or figuring out the drain in energy from resistance combined with oscillation in an electrical system.
Complex numbers with imaginary components also are useful in theoretical physics, explains Rolando Somma, a physicist who works in quantum computing algorithms at Los Alamos National Laboratory.
"Due to their relation with trigonometric functions, they are useful for describing, for example, periodic functions," Somma says via email. "These arise as solutions to the wave equations, so we use complex numbers to describe various waves, such an electromagnetic wave. Thus, as in math, complex calculus in physics is an extremely useful tool for simplifying calculations."
Complex numbers also have a role in quantum mechanics, a theory that describes the behavior of nature at the scale of atoms and subatomic particles.
"In quantum mechanics i appears explicitly in Schrödinger's equation," Somma explains. "Thus, complex numbers appear to have a more fundamental role in quantum mechanics rather than just serving as a useful calculational tool."
"The state of a quantum system is described by its wave function," he continues. "As a solution to Schrodinger's equation, this wave function is a superposition of certain states, and the numbers appearing in the superposition are complex. Interference phenomena in quantum physics, for example, can be easily described using complex numbers."
This article was updated in conjunction with AI technology, then fact-checked and edited by a HowStuffWorks editor.
Advertisement
Please copy/paste the following text to properly cite this HowStuffWorks.com article:
Advertisement