Next to E = mc², F = ma is the most famous equation in all of physics. Yet many people remain mystified by this fairly simple algebraic expression. It's actually a mathematical representation of Isaac Newton's second law of motion, one of the great scientist's most important contributions. The "second" implies that other laws exist, and, luckily for students and trivia hounds everywhere, there are only two additional laws of motion. Here they are:
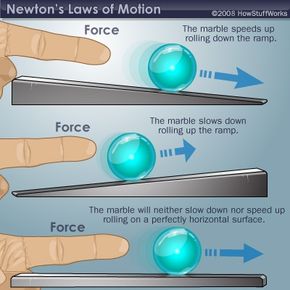
- Every object persists in its state of rest or uniform motion — in a straight line unless it is compelled to change that state by forces impressed on it.
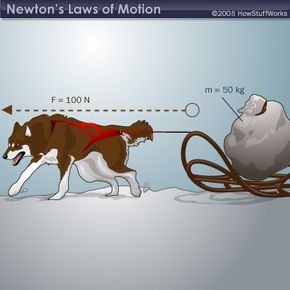
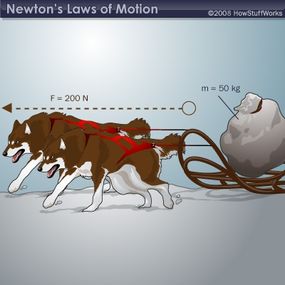
- Force is equal to the change in momentum per change in time. For a constant mass, force equals mass times acceleration.
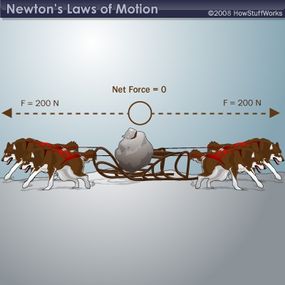
- For every action, there is an equal and opposite reaction.
These three laws form the foundation of what is known as classical mechanics, or the science concerned with the motion of bodies related to the forces acting on it. The bodies in motion could be large objects, such as orbiting moons or planets, or they could be ordinary objects on Earth's surface, such as moving vehicles or speeding bullets. Even bodies at rest are fair game.
Advertisement
Where classical mechanics begins to fall apart is when it tries to describe the motion of very small bodies, such as electrons. Physicists had to create a new paradigm, known as quantum mechanics, to describe the behavior of objects at the atomic and subatomic level.
But quantum mechanics is beyond the scope of this article. Our focus will be classical mechanics and Newton's three laws. We'll examine each in detail, both from a theoretical and a practical point of view. We'll also discuss the history of Newton's laws, because how he arrived at his conclusions is just as important as the conclusions themselves. The best place to start, of course, is at the beginning with Newton's first law.
Advertisement