How Carbon-14 Dating Works

t rex — Paleontologists of the Natural History Museum of Los Angeles prepare and assemble the fossils of a 66 million year-old Tyrannosaurus rex nicknamed Thomas, in Los Angeles on March 27, 2008. This T-Rex specimen is estimated to be a 70% complete and one of 30 partially complete T-Rex fossils worldwide. Thomas was excavated in Montana between 2003 and 2005. GABRIEL BOUYS/AFP/Getty Images

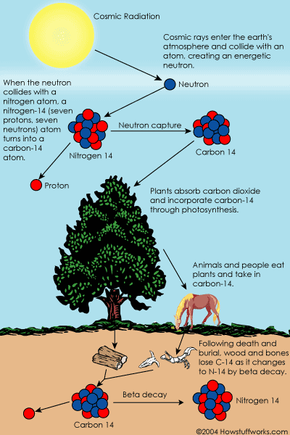
You probably have seen or read news stories about fascinating ancient artifacts. At an archaeological dig, a piece of wooden tool is unearthed and the archaeologist finds it to be 5,000 years old. A child mummy is found high in the Andes and the archaeologist says the child lived more than 2,000 years ago. How do scientists know how old an object or human remains are? What methods do they use and how do these methods work? In this article, we will examine the methods by which scientists use radioactivity to determine the age of objects, most notably carbon-14 dating.

Carbon-14 dating is a way of determining the age of certain archeological artifacts of a biological origin up to about 50,000 years old. It is used in dating things such as bone, cloth, wood and plant fibers that were created in the relatively recent past by human activities.

Contents

How Carbon-14 is Made
Dating a Fossil

How Carbon-14 is Made

Cosmic rays enter the earth's atmosphere in large numbers every day. For example, every person is hit by about half a million cosmic rays every hour. It is not uncommon for a cosmic ray to collide with an atom in the atmosphere, creating a secondary cosmic ray in the form of an energetic neutron, and for these energetic neutrons to collide with nitrogen atoms. When the neutron collides, a nitrogen-14 (seven protons, seven neutrons) atom turns into a carbon-14 atom (six protons, eight neutrons) and a hydrogen atom (one proton, zero neutrons). Carbon-14 is radioactive, with a half-life of about 5,700 years.

For more information on cosmic rays and half-life, as well as the process of radioactive decay, see How Nuclear Radiation Works.

Carbon-14 in Living Things

The carbon-14 atoms that cosmic rays create combine with oxygen to form carbon dioxide, which plants absorb naturally and incorporate into plant fibers by photosynthesis. Animals and people eat plants and take in carbon-14 as well. The ratio of normal carbon (carbon-12) to carbon-14 in the air and in all living things at any given time is nearly constant. Maybe one in a trillion carbon atoms are carbon-14. The carbon-14 atoms are always decaying, but they are being replaced by new carbon-14 atoms at a constant rate. At this moment, your body has a certain percentage of carbon-14 atoms in it, and all living plants and animals have the same percentage.

Dating a Fossil

As soon as a living organism dies, it stops taking in new carbon. The ratio of carbon-12 to carbon-14 at the moment of death is the same as every other living thing, but the carbon-14 decays and is not replaced. The carbon-14 decays with its half-life of 5,700 years, while the amount of carbon-12 remains constant in the sample. By looking at the ratio of carbon-12 to carbon-14 in the sample and comparing it to the ratio in a living organism, it is possible to determine the age of a formerly living thing fairly precisely.

A formula to calculate how old a sample is by carbon-14 dating is:

t = [ ln (Nf/No) / (-0.693) ] x t1/2

t = [ ln (N_f/N_o) / (-0.693) ] x t_1/2

where ln is the natural logarithm, N_f/N_o is the percent of carbon-14 in the sample compared to the amount in living tissue, and t_1/2 is the half-life of carbon-14 (5,700 years).

So, if you had a fossil that had 10 percent carbon-14 compared to a living sample, then that fossil would be:

t = [ ln (0.10) / (-0.693) ] x 5,700 years

t = [ (-2.303) / (-0.693) ] x 5,700 years

t = [ 3.323 ] x 5,700 years

t = 18,940 years old

Because the half-life of carbon-14 is 5,700 years, it is only reliable for dating objects up to about 60,000 years old. However, the principle of carbon-14 dating applies to other isotopes as well. Potassium-40 is another radioactive element naturally found in your body and has a half-life of 1.3 billion years. Other useful radioisotopes for radioactive dating include Uranium -235 (half-life = 704 million years), Uranium -238 (half-life = 4.5 billion years), Thorium-232 (half-life = 14 billion years) and Rubidium-87 (half-life = 49 billion years).

The use of various radioisotopes allows the dating of biological and geological samples with a high degree of accuracy. However, radioisotope dating may not work so well in the future. Anything that dies after the 1940s, when Nuclear bombs, nuclear reactors and open-air nuclear tests started changing things, will be harder to date precisely.

Originally Published: Oct 3, 2000

Carbon-14 Dating FAQs

How accurate is carbon-14 dating?

Advances in technology has made it possible to date objects and materials so it is only off by a few decades, at most.

How is carbon-14 used to date fossils?

All living things absorb carbon from the atmosphere, including an amount of radioactive carbon-14. When that plant or animal dies, it stops absorbing carbon. But the radioactive carbon-14 it has accumulated continues to decay. Scientists can measuring the amount of carbon-14 left over and estimate how long ago the plant or animal died.

Where is carbon-14 found?

All living things absorb carbon from the atmosphere, including an amount of radioactive carbon-14. It is mostly found in atmospheric carbon dioxide because that is where it is constantly being produced by collisions between nitrogen atoms and cosmic rays.

What things can carbon-14 dating be used for?

Carbon-14 dating can be used to determine the age of everything from bones and plant fibers, to wood and pollen.

Is carbon-14 harmful to humans?

No. Even large, external exposure to amounts of the isotope don't pose any risk to people. The radiation hardly penetrates the outermost layer of skin on the body.