Science and Nature: Fractals

The most famous of all the fractals is the Mandelbrot set. Mathematician Benoit Mandelbrot coined the term "fractal" in 1975 to name a new category of math which quantifies geometric irregularities and the order within seemingly chaotic shapes.

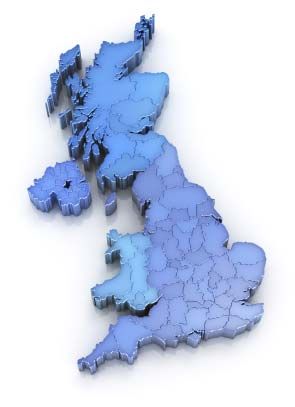
Long before Mandelbrot gave fractal geometry a name, mathematicians were grappling with the concepts related to the fractal dimension. While studying the coast of England in the first half of the 20th century, Lewis Fry Richardson realized that the smaller the ruler, the longer the coastline measurement would be. As your measuring tool decreases, it is able to capture more of the details of a jagged shape's outline. In fractal terms, the coastline of England is infinite.

The Menger Sponge was developed by Karl Menger while exploring the quantification of topological dimension. It may be less artistically thrilling than most images of the Mandelbrot and Julia sets, but use of the Menger Sponge formula has advanced many areas of science.

Nature is loaded with fractal shapes. This fern leaf exhibits one of the key characteristics of fractals: self-similarity. Each tiny leaflet is curled into a shape which mimics the larger frond.

Nautilus shells are an example of Mother Nature showing off her geometry skills. Each chamber is a smaller iteration of the one that precedes it; in fractal geometry formulas, this characteristic is represented as a feedback loop, where the result of one iteration of the formula becomes a variable for the next iteration.

Eat your geometry! Romansco broccoli grows in such a structured repetitive pattern that you may be inclined to think it's engineered to do so by evil scientists bent on vegetable domination. Nope! Nature takes care of all the math.

Looking very closely at a snowflake, you'll see that the features of each branch of its shape look the same as the flake as a whole (at least until it melts). Finding and quantifying these ordered structures within what initially appears random is one of fractal geometry's primary objectives.

This is NOT a magnified snowflake; it's a fractal equation represented visually. The similarities between naturally-occurring fractals and those created mathematically illustrate the close correlation of the two in this branch of geometry.

While nature offers up innumerable examples of fractal loveliness, once fractal formulas were expressed visually by plotting their values on a complex number plane, a new art genre was born.

Mathematician Gaston Julia is credited with developing the concept of the feedback loop used in fractal geometry. His work in the early 1900s was limited by a lack of a computer to perform the calculations of his formula, the Julia set. Today, digital artists use variations of the Julia set to create works of art like this one. Imagine what Julia would have done with 21st century computing power!

By changing the variables in a fractal equation, you can create infinite variations on a theme. If you look closely at this image, you'll see smaller and smaller iterations of the Mandelbrot set.

As you look at visual representations of fractal equations, you begin to see how natural all that "chaos" looks. The blue color of this fractal render makes it easy to see its similarities to a craggy coastline.

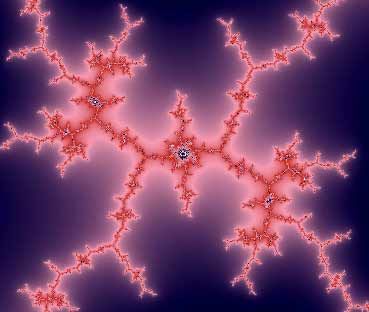
Graphed variations of the Mendelbrot set often have segments of lightning-like tendrils, and that's no coincidence -- lightning is a naturally occurring fractal.

If you were to zoom in on the smaller arms of this rendering of the Julia set, you'd see that they look exactly like the larger image. This self-similarity plays out infinitely in computer-generated fractal models, whereas fractals occurring in nature normally run through a limited number of iterations.

Remember those hidden image stereograms that were so popular in the 1990s? If you stare at what appears to be a busy, repeating pattern, eventually a 3-D image should become visible. Some creators of these works of art use fractals as the basis of their backgrounds. This image looks as though it could be stereographic, but in fact it's just a normal fractal.

Finally, an example of how fractal geometry can be both beautiful and practical. This outdoor exhibit was constructed using fractals to create a heat-dissipating sunshade in Tokyo. The angles created by using fractal tetrahedrons disperse heat more efficiently than a flat-roofed shade. Learn more about How Fractals Work.