How Game Theory Works

Using a Game Tree

In a previous section, we examined the prisoner's dilemma and plotted it on a matrix. That was an example of a simultaneous-move game. Games are either simultaneous-move or sequential-move games. In simultaneous-move games, both players make a move without knowledge of the other players' moves. A blind auction works this way, as does bidding for contracts. In sequential-move games, the players take turns moving, as in chess or negotiations.

For games in which both players move simultaneously, we must assume our opponent is going to seek the best outcome possible. Therefore, we must protect ourselves by also making the most advantageous move possible. Would players choose different strategies in the prisoner's dilemma if it was played sequentially instead of simultaneously?

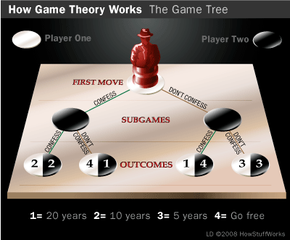
While simultaneous-move games can be plotted on matrices, sequential-move games can be plotted on game trees. The prisoner's dilemma mapped out on a game tree would look like this:

The order of moves is represented top-to-bottom on the tree. The uppermost node represents the first move of Player 1 (confessing or not confessing). The two nodes below it are subgames. Each represents Player 2's possible reaction to the first move made. The four nodes on the bottom row are terminal nodes and represent all four possible payoffs to this particular game.

We're able to look at the game in this form and choose the best strategy for the player making the final move in the game, which is Player 2. This allows us to work backwards to determine what move Player 1 should make, knowing how Player 2 will rationally behave in either scenario. This process of looking at the game from end-to-beginning is called backward induction. We see that Player 2's best strategy is to confess, regardless of Player 1's opening move. By moving our analysis further up the tree, to the beginning of the game, we know that Player 1 must choose defection (confession).

We see that in a one-shot game like prisoner's dilemma that playing simultaneously or sequentially doesn't change the optimal strategy for each player.

In the next section, we'll learn why perfectly rational selfishness must be thrown out the window when we play prisoner's dilemma over and over.

The best cure is none at all?

Schizophrenia -- a mental illness that affects thoughts, perceptions and behaviors -- first afflicted mathematician John Nash in the late 1950s. For years, Nash went in and out of hospitals for treatment of his disease. In 1970, he changed his strategy and stopped taking antipsychotic drugs entirely. Nash made a remarkable and near-complete recovery from schizophrenia.

The World Health Organization (WHO) found that schizophrenic patients in undeveloped countries have a better long-term outlook than those in developed nations. Five years after diagnosis, about two-thirds of schizophrenics in poorer nations (where antipsychotic drugs are less available) have shown improvement and 40 percent have essentially recovered [source: Whitaker]. Patients in developed countries, however, have a higher risk of becoming chronically ill. Schizophrenics in areas where pharmacological treatment is unavailable are 10 times less likely to have a recurrence of the illness [source: James]. The WHO even declared that living in a developed nation is a "strong predictor" that schizophrenia will be chronic in a patient.