Rhombus Properties and Perimeter Formula

A pattern of blue and green rhombus tiles — Once you're familiar with the rhombus, you start seeing it in patterns everywhere. shuoshu / Getty Images

Key Takeaways

Rhombus is a parallelogram with four equal sides, also known as an equilateral quadrilateral.
Not all parallelograms are rhombuses; squares are a type of rhombus with equal interior angles.
Rhombus properties include equal side lengths, parallel opposite sides, equal opposite angles, adjacent angles totaling 180 degrees and diagonals bisecting at 90 degrees.

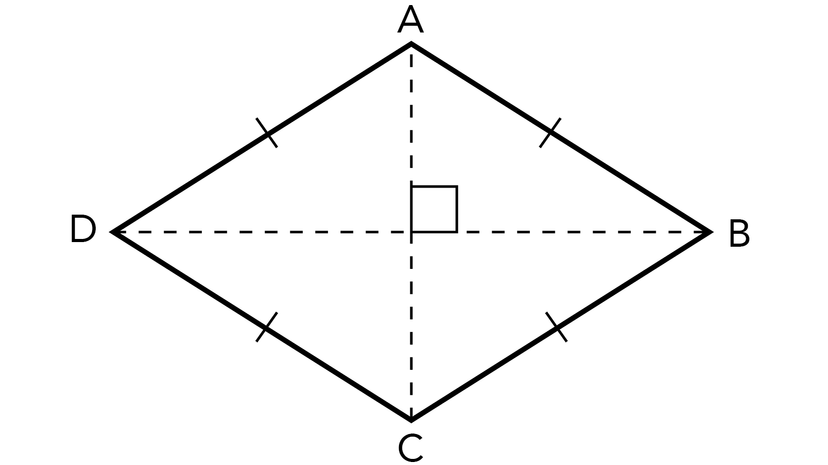
A rhombus is a parallelogram shape with two pairs of parallel sides and four equal sides. These four sides of equal length also define the rhombus as an equilateral quadrilateral. Etymologically, the name of this shape stems from the Greek word "rhombos," which roughly translates to "spinning top."

The easiest way to picture a rhombus would be to draw a diamond on a two-dimensional plane and label each point with a letter from the alphabet. With each line joining points A, B, C and D, you'll create the four sides of a rhombus that you can use as a visual to help visualize the following information.

Is a Square a Rhombus?

In short, sometimes. Every rhombus is a parallelogram, but not every parallelogram is a rhombus. Both rhombuses and squares have four sides that are all the same length, but a square is a regular polygon with equal interior angles (meaning all the interior angles share the same measurement).

Simple drawing of a rhombus with the sides and diagonals marked — Rhombus ABCD.
Dream01/shutterstock

Looking at rhombus ABCD, you'll notice that two adjacent sides of a diamond shape don't necessarily have equal interior angles. They may be equal in the figure you drew on paper, but only the opposite interior angles of a rhombus must match.

5 Rhombus Traits

Real-life examples of rhombuses can include kites or a rhombus-shaped tile that meets the basic properties of the shape. Read through the following properties to gain a better understanding of how to identify rhombuses when you encounter them.

1. All Sides Are of Equal Length

The first property of a rhombus is that all four sides are the same length. Judging the side length may be difficult if the diamond shape is somewhat distorted with various interior angles. However, if you use a ruler, you'll find that every line of a true rhombus has equal lengths.

2. Opposite Sides Are Parallel

The second property of a rhombus refers to its "opposite sides equal, opposite sides parallel" categorization as a parallelogram. "Parallel" means that two opposite lines are drawn at the same angle. So, if you were to extend these lines and draw them for infinity, they would never touch.

3. Opposite Angles Are Equal

Opposite interior angles (and only the opposite angles) of a rhombus must match. Redraw rhombus ABCD in various ways, and you can guarantee that opposite angles equal each other every time. This is, of course, another separation between squares and rhombuses, as squares have four equal angles.

4. Adjacent Angles Equal 180 Degrees

One of the basic principles of a rhombus is any two adjacent angles will equal 180 degrees. Knowing this, as well as the fact that all angles must add up to a total of 360 degrees, will help you solve geometry equations with unknown angles.

5. All Diagonals of a Rhombus Bisect at 90 Degrees (Perpendicular Bisector)

Illustrate the diagonals of a rhombus by drawing two lines connecting endpoints from each opposite side of rhombus ABCD. You'll see that the two diagonals bisect somewhere in the middle. Measure the crosshair shape where the perpendicular diagonals meet with a protractor.

These diagonal bisects should create four right-angle L-shapes equal to 90 degrees.

How Do You Find the Perimeter of a Rhombus?

To find the perimeter (total length) of a rhombus, add all its sides together.

Area = A + B + C + D

If you are given a math problem to find the missing lengths of quadrilateral ABCD, and you only know the lengths of lines BC and CD, remember that all sides are equal lengths. Simply multiply one known side by 4 to solve.