What Is a Perfect Square?

A perfect square is a special type of number that you get by multiplying another number by itself. It's like the mathematical equivalent of a square shape — neat, balanced, and intriguing.

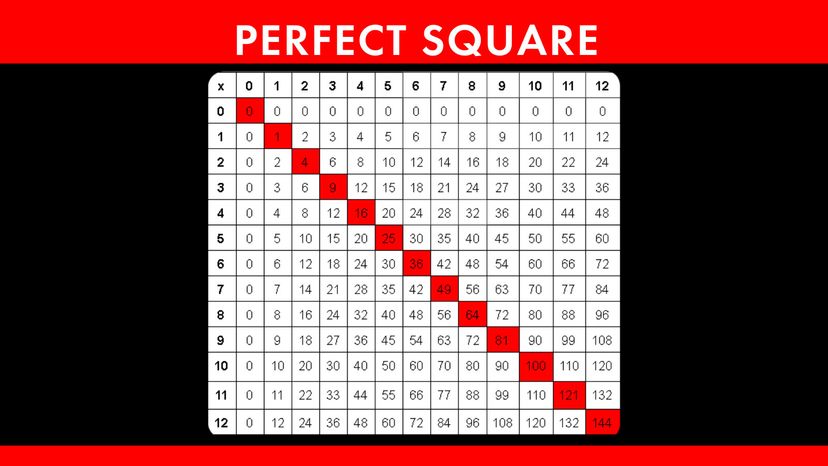
To illustrate, when you multiply 5 by 5, you get 25, making 25 a perfect square because it's the result of 5 x 5.

So, how can you determine if a number is a perfect square? The trick lies in finding its square root, which is the reverse operation of squaring a number. If the square root yields a whole number, you're looking at a perfect square.

For instance, the square root of 16 is 4 because 4 x 4 = 16. Therefore, 16 is indeed a perfect square. Likewise, if you calculate the square root of 144, you'll find it's 12 because 12 x 12 = 144. Bingo! Another perfect square.

Perfect Squares Chart

To help you get a better grasp of perfect squares, here are a few more common examples:

As you can see, each of these numbers can be expressed as the product of two equal integers, making them perfect squares.

Now that we've defined perfect squares and how to identify them, let's explore a few more details to deepen our understanding.

When examining perfect squares, notice a fascinating pattern: The units place digit of a perfect square is always 0, 1, 4, 5, 6, or 9. This characteristic can be quite handy when identifying perfect squares quickly.

If you want to go a step further and find perfect squares manually, you can use long multiplication method.

Perfect squares are not limited to small numbers; they extend far beyond. For instance, 625 is a perfect square because it's the result of 25 x 25. Exploring larger perfect squares can be a fun mathematical journey.

Perfect squares are not just mathematical curiosities; they have real-world applications in various fields, including geometry and algebra. Understanding them can open doors to a deeper appreciation of mathematics.

This article was updated in conjunction with AI technology, then fact-checked and edited by a HowStuffWorks editor.