30-60-90 Triangle: 4 Facts to Remember for Your Next Test

A triangle with angles of 30,60 and 90 degrees on a white background — Thankfully, the 30-60-90 triangle is pretty straightforward. The largest angle in this shape is the 90-degree angle, which will always be adjacent to the shortest leg and opposite the hypotenuse. KRPD / Shutterstock

Anyone who's ever faced mind-numbing trigonometry problems and practice questions will be familiar with the Pythagorean Theorem and its square root principles in the 30-60-90 triangle. This special triangle has several short-cut rules to help new mathematicians find interior angles and linear lengths quickly.

All triangles have interior angle sums equal to 180 degrees, but special triangles (like right triangles and equilateral triangles) are the easiest to solve in geometry practice problems and other homework assignments because there is a consistent relationship between angles with the same ratio each time.

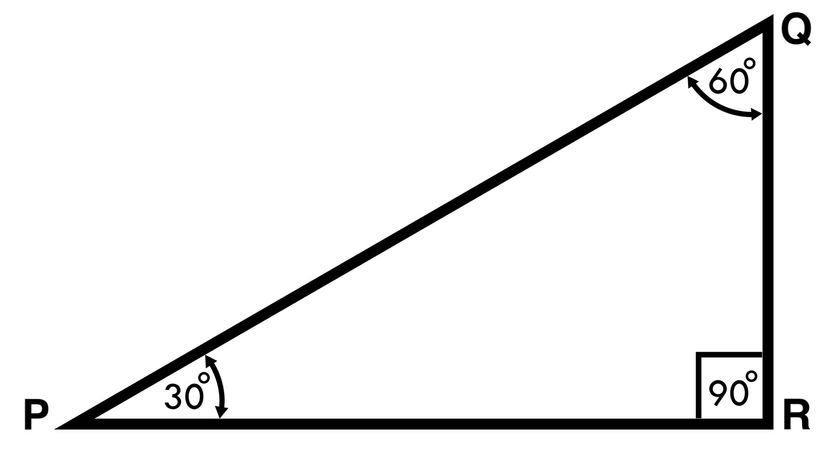
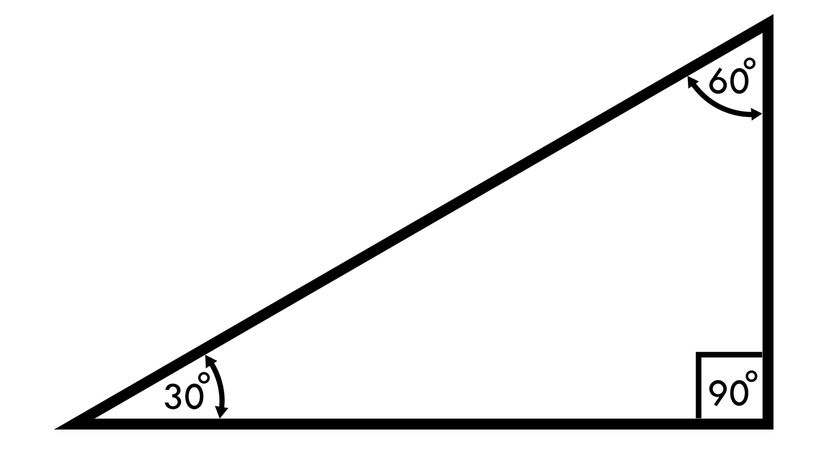
Let's look at the hypothetical triangle PQR to illustrate some of the key characteristics of a 30-60-90 triangle.

Contents

A 30-60-90 Triangle Is Always a Right Triangle
The Hypotenuse Is Twice the Length of the Smallest Side
The Smallest Angle Is 30 Degrees
The Midsized Angle Is Always 60 Degrees

1. A 30-60-90 Triangle Is Always a Right Triangle

Triangle with the 30 angle labeled as P, 60 as Q, and 90 as R — Triangle PQR. KRPD / Shutterstock

PQR is a special right triangle. All the sides and angles of this right-angled triangle (90 degrees) are uneven, unlike an equilateral triangle with equal angles or an isosceles triangle with two even legs.

However, by bisecting an isosceles triangle at the angle where the two identical sides meet, you can create two identical right triangles.

2. The Hypotenuse Is Twice the Length of the Smallest Side

If the problem provides one of two side lengths (the longest side, aka the hypotenuse, or the shortest side) you can easily find the other side length.

If problem states the length of the hypotenuse, you can divide that value by 2 to find the length of the shortest leg. If the problem provides the short leg dimension, you can multiply that measurement by 2 to find the hypotenuse.

3. The Smallest Angle Is 30 Degrees

The smallest angle of a 30-60-90 triangle is always 30 degrees and is adjacent to the longest side (hypotenuse). The other long leg leading from 30 degrees to the right angle equals the √3 times the length of the shortest side.

4. The Midsized Angle Is Always 60 Degrees

Remember that the middle-length leg is always opposite the 60-degree angle. Therefore, once you identify the medium-length angle, you can quickly pinpoint the remaining angle equal to 30 degrees.