Even the Smartest Mathematicians Can't Solve the Collatz Conjecture

Key Takeaways

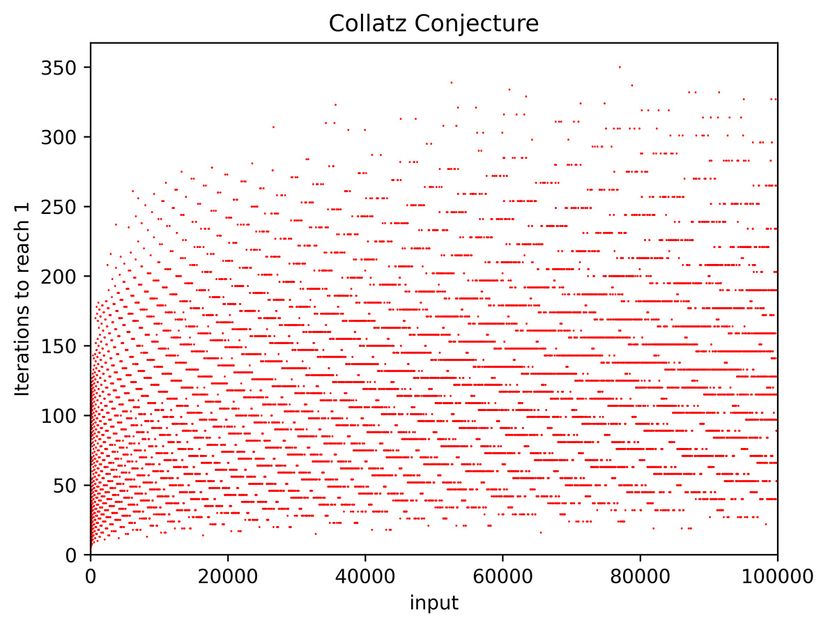
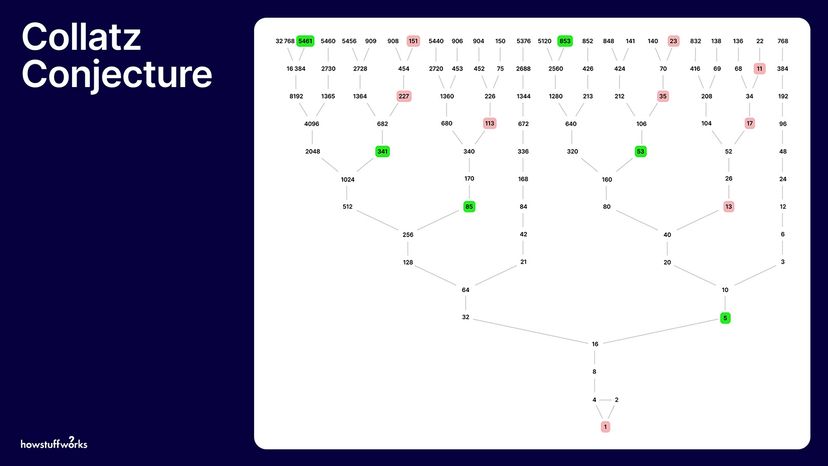
The Collatz Conjecture, also known as the "3n + 1" sequence, proposes that starting with any positive number and applying two rules (if even, divide by two; if odd, triple it and add one) will always eventually lead to the number one.
This simple mathematical puzzle has eluded a formal proof, captivating mathematicians for decades with its straightforward concept yet complex behavior leading to an unpredictable sequence.
Despite its simplicity, the conjecture remains one of mathematics' unsolved problems, demonstrating the intricate nature of numbers and the challenges of proving seemingly simple patterns.

Mathematicians are in the business of solving problems. In the process of these problem-solving attempts, they explore ideas and sometimes come up with other math problems to tinker with. Some of these problems can take generations of mathematicians their entire careers to solve, and some require the help of a supercomputer. Others seem just plain unsolvable — although the general consensus is that we should be able to sort out all math problems eventually.

The History of the Unsolved Math Problem

The Collatz conjecture, or the "3n+1 problem," is one we're still waiting to see solved. Introduced in 1937 by German mathematician Lothar Collatz, the Collatz conjecture is a seemingly straightforward question with a surprisingly elusive answer. The conjecture posits that if you repeat two simple arithmetic operations, you will eventually end up transforming every positive integer into the number one. The problem is that it has not yet been proven to be true for all integers. Maybe with some number the sequence gallops off into infinity.

Mathematicians have tested millions of natural numbers, and nobody's proved it wrong. But nobody's proved it unconditionally correct, either. Legendary Hungarian mathematician Paul Erdos is quoted as saying, "Mathematics may not be ready for such problems."

Collatz came up with his conjecture just two years after receiving his doctorate from the University of Berlin. For someone who did so much important mathematical work in his career, that he's known for a novelty problem — one that could be tested by a group of fourth graders — is remarkable. While all calculations support the idea that the conjecture is true, the fact that it has remained unsolved for 86 years makes it all the more intriguing.

Why Is the Collatz Conjecture Also Called the '3n + 1' Sequence?

The Collatz sequence is also called the "3n + 1" sequence because it is generated by starting with any positive number and following just two simple rules: If it's even, divide it by two, and if it's odd, triple it and add one. Hence, "3n + 1." Follow those two rules over and over, and the conjecture states that, regardless of the starting number, you will always eventually reach the number one.

For example, start with the number seven. It's an odd number, so you give it the old 3n + 1 treatment, which equals 22. That's an even number, which means you've got to cut it in half, which gives us 11. Here's the calculation for rest of the sequence:

11 x 3 = 33 + 1 = 34 34 / 2 = 17 17 x 3 = 51 + 1 = 52 52 / 2 = 26 26 / 2 = 13 13 x 3 = 39 + 1 = 40 40 / 2 = 20 20 / 2 = 10 10 / 2 = 5 5 x 3 = 15 + 1 = 16 16 / 2 = 8 8 / 2 = 4 4 / 2 = 2 2 / 2 = 1

So, if you start with the number seven, the Collatz sequence is 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. If you do it again from the number one, an odd number, you multiply by three and add one. From there you get four, which quickly reduces back to one. This begins the loop that never ends.

Limited Breakthroughs With the 'Hailstone Sequence'

Another name for the numbers generated in the Collatz conjecture is the "hailstone sequence." As you can see from the sequence listed above, the numbers go up and down and up and down like hailstones in a storm cloud, being lofted up, collecting ice and, after falling into a lower part of the cloud, blown upward again. At some point they plummet to the ground. There are certain numbers that, once you reach them in your calculations, fall most rapidly, but they all fall eventually to one.

So, the Collatz conjecture works for millions upon millions of numbers — anything with fewer than 19 digits, in case you were thinking about trying your luck with anything smaller — but one of the problems mathematicians are trying to solve is why. If they understood that, they would have a way of saying with certainty that it works on all natural numbers.

One thing that makes the Collatz conjecture so confounding is that it involves an infinite number of integers. Even the most powerful supercomputer can't check every single number to see if the conjecture holds true. Not yet, at least.

One mathematician in recent years has made a bit of a breakthrough on the Collatz conjecture. Terence Tao, one of the most gifted mathematicians of the past century, published a paper in 2019 titled "Almost All Collatz Orbits Attain Almost Bounded Values." Tao is no slouch — he earned his Ph.D. from Princeton at the age of 21 and became the youngest-ever math professor at UCLA at 24. He won the Fields Medal, the highest math award in all the land, at the age of 31. And yet his big news about his Collatz breakthrough has two "almosts" in it.

Basically, Tao's results point to a new method for approaching the problem and note how rare it would be for a number to diverge from the Collatz rule. Rare, but not necessarily nonexistent.

And that, friends, is the closest anybody's come in recent years to solving the Collatz conjecture. Remember, if you're going to try to solve it yourself, begin with numbers starting with at least 20 digits.