How Nuclear Power Works

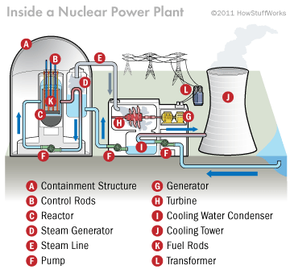
In order to turn nuclear fission into electrical energy, nuclear power plant operators have to control the energy given off by the enriched uranium and allow it to heat water into steam. That steam then drives turbines to generate electricity [source: NEI].

Enriched uranium typically is formed into 1-inch-long (2.5-centimeter-long) pellets, each with approximately the same diameter as a dime. Next, the pellets are arranged into long rods, and the rods are collected together into bundles. The bundles are submerged in water inside a pressure vessel. The water acts as a coolant. Left to its own devices, the uranium would eventually overheat and melt.

To prevent overheating, control rods made of a material that absorbs neutrons are inserted into the uranium bundle using a mechanism that can raise or lower them. Raising and lowering the control rods allow operators to control the rate of the nuclear reaction. When an operator wants the uranium core to produce more heat, the control rods are lifted out of the uranium bundle (thus absorbing fewer neutrons). To reduce heat, they are lowered into the uranium bundle. The rods can also be lowered completely into the uranium bundle to shut the reactor down in the event of an accident or to change the fuel [sources: Nosowitz, World-nuclear.org].

The uranium bundle acts as an extremely high-energy source of heat. It heats the water and turns it to steam. The steam drives a turbine, which spins a generator to produce power. Humans have been harnessing the expansion of water into steam for hundreds of years.

In some nuclear power plants, the steam from the reactor goes through a secondary, intermediate heat exchanger to convert another loop of water to steam, which drives the turbine. The advantage to this design is that the radioactive water/steam never contacts the turbine. Also, in some reactors, the coolant fluid in contact with the reactor core is gas (carbon dioxide) or liquid metal (sodium, potassium); these types of reactors allow the core to be operated at higher temperatures [source: World-nuclear.org]

Given all the radioactive elements inside a nuclear power plant, it shouldn't come as a surprise that there's a little more to a plant's exterior than you'd find at a coal power plant. In the next section, we'll explore the various protective barriers between you and the atomic heart of the plant.