Time Dilation
In order to attempt to prove this theory of time dilation, two very accurate atomic clocks were synchronized and one was taken on a high-speed trip on an airplane. When the plane returned, the clock that took the plane ride was slower by exactly the amount Einstein's equations predicted. Thus, a moving clock runs more slowly when viewed by a frame of reference that is not in motion with it. Keep in mind that when the clock returned, it had recorded less time than the ground clock. Once re-united with the ground clock, the slow clock will again record time at the same rate as the ground clock (obviously, it will remain behind by the amount of time it slowed on the trip unless re-synchronized). It is only when the clock is in motion with respect to the other clock that the time dilation occurs. Take a look at Fig 4 and Fig 5 below.
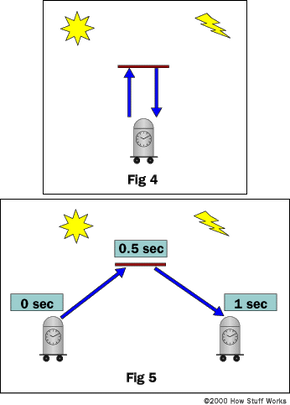
Let's assume that the object under the sun in Fig 4 is a light clock on wheels. A light clock measures time by sending a beam of light from the bottom plate to the top plate where it is then reflected back to the bottom plate. A light clock seems to be the best measure of time since its speed remains constant regardless of motion. So in Fig 4, we walk up to the light clock and find that it takes 1 sec for the light to travel from the bottom to the top and back to the bottom again. Now look at Fig 5. In this example, the light clock is rolling to the right, but we are standing still. If we could see the light beam as the clock rolled past us, we would see the beam travel at angles to the plates. If you are confused, look at Fig 4 and you'll see that both the sent beam and received beam occur under the sun, thus the clock is not moving. Now look at fig 5, the sent beam occurs under the sun, but the reflected beam returns when the clock is under the lightning bolt, thus the clock is rolling to the right. What is this telling us? We know that the clock standing still sends and receives at 1-second intervals. We also know that the speed of light is constant. Regardless of where we are, we would measure the light beam in fig 4 and fig 5 to be the exact same speed. But Fig 5 looks like the light traveled farther because the arrows are longer. And guess what, it did. It took the light longer to make one complete send and receive cycle, but the speed of the light was unchanged. Because the light traveled farther and the speed was unchanged, this could only mean that the time it took was longer. Remember speed is distance / time, so the only way for the speed to be unchanged when the distance increases is for the time to also increase.
Advertisement
We'll look at time intervals in the next section.