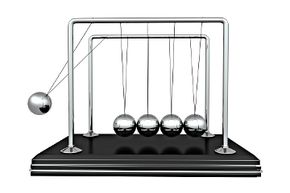
You've probably seen this contraption before: Five small silver balls hang in a perfectly straight line by thin threads that attach them to two parallel horizontal bars, which are in turn attached to a base. They sit on office desks around the world.
If you pull a ball up and out and then release it, it falls back and collides with the others with a loud click. Then, instead of all four remaining balls swinging out, only the ball on the opposite end jumps forward, leaving its comrades behind, hanging still. That ball slows to a stop and then falls back, and all five are briefly reunited before the first ball is pushed away from the group again.
Advertisement
This is a Newton's cradle, also called a Newton's rocker or a ball clicker. It was so-named in 1967 by English actor Simon Prebble, in honor of his countryman and revolutionary physicist Isaac Newton.
Despite its seemingly simple design, the Newton's cradle and its swinging, clicking balls isn't just an ordinary desk toy. It is, in fact, an elegant demonstration of some of the most fundamental laws of physics and mechanics.
The toy illustrates the three main physics principles at work: conservation of energy, conservation of momentum and friction. In this article, we'll look at those principles, at elastic and inelastic collisions, and kinetic and potential energy. We'll also examine the work of such great thinkers as Rene Descartes, Christiaan Huygens and Isaac Newton himself.
Advertisement