According to Hubble's classification system, the Milky Way is a spiral galaxy, although more recent mapping evidence indicates that it may be a barred spiral galaxy.
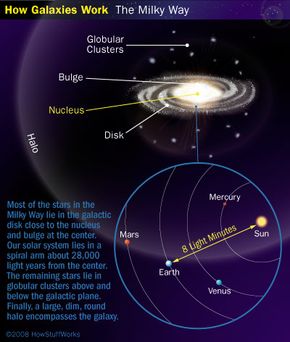
The Milky Way has more than hundreds of billions of individual stars. It's approximately 100,000 light-years in diameter, and the sun is located about 28,000 light years from the center. If we look at the structure of the Milky Way as it would appear from the outside, we can see certain parts.
Galactic Disk
The Milky Way's disk consists of both old and young stars, with plentiful gas and dust. Stars in the disk orbit the galactic center in near-circular paths, with slight vertical motion due to gravitational interactions, resembling merry-go-round horses.
The disk has three regions: the nucleus at the center, the bulge around the nucleus extending slightly above and below the disk's plane and the spiral arms radiating outward. Our solar system is located in one of these arms, specifically the Orion Arm. Other arms include the Perseus Arm, Sagittarius Arm and Scutum-Centaurus Arm.
Globular Clusters
Several hundred globular clusters are scattered above and below the plane of the galactic disk, orbiting the galactic center in elliptical paths with randomly scattered directions.
The stars within these clusters are significantly older compared to those in the galactic disk, and the clusters contain little to no gas and dust.
Halo
The halo, a large, dim area surrounding the galaxy, comprises hot gas, dark matter and old stars. Despite the apparent mass in the galaxy's disk and center, rotation curve studies reveal most mass resides in the halo, hinting at dark matter's presence.
The Milky Way's gravity affects two satellite galaxies, the Large and Small Magellanic Clouds, visible from the Southern Hemisphere and orbiting at varying positions around our entire galaxy.
The Large Magellanic Cloud, about 14,000 light-years in diameter and 163,000 light-years away, may lose gas and dust to the Milky Way due to gravitational interactions.
Luminosity-distance Relationship
Astronomers use devices like photometers on telescopes to measure a star's brightness. Knowing a star's brightness and distance allows them to compute its luminosity using the formula: luminosity = brightness x 12.57 x (distance)².
Luminosity can also indicate a star’s distance from Earth. Stars like RR Lyrae and Cepheid variables, which change brightness predictably, serve as benchmarks.
To determine the luminosities of the globular clusters, Shapely measured the periods of brightness of the RR Lyrae stars in the clusters. Once he knew the luminosities, he could calculate their distances from Earth.