Math Concepts

A reinterpretation of an ancient Babylonian tablet shows that trigonometry might be 1,000 years older than thought. But there's some disagreement.

By Jesslyn Shields

With a little patience, you can master this trick of converting binary code to decimals - and have fun doing it!

By Mark Mancini

Has this ever happened to you? The meteorologist calls for a massive snowstorm, but the flakes fail to arrive. Chaos theory can shed light on why forecasts fail (and why our orderly world may not be so orderly after all).

By William Harris

Mathematics achieves the sublime. Sometimes, as with tessellations, it rises to art. In their simplest form, tessellations consist of a single shape that repeats over a two-dimensional plane without any gaps. Why was M.C. Escher so fixated on them?

By Nicholas Gerbis

Fractals have been around forever but were only defined in the last quarter of the 20th century. Think you can wrap your brain around how fractals work?

By Craig Haggit & Yara Simón

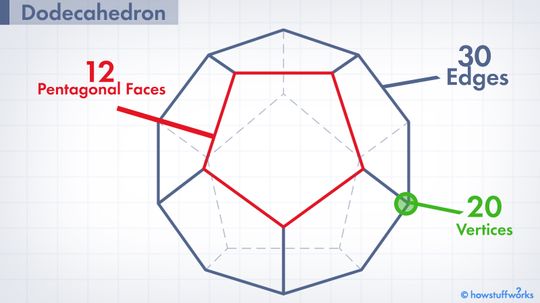
A dodecahedron has 12 flat faces, all shaped like pentagons. Here are 12 cool things you just may not know about them.

By Mark Mancini

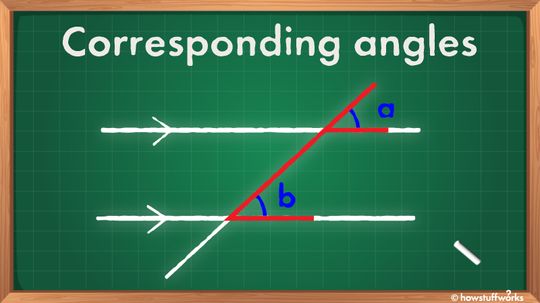
Corresponding angles are what you get when two parallel lines are crossed by a third line, creating angles that have the same relative position at each intersection. They're easy to find once you know what to look for.

By Nathan Chandler & Austin Henderson

We may think the butterfly effect means that a small change (like the flap of a butterfly's wings) can have huge consequences (a tornado in China). But what if it means the opposite?

By Nathan Chandler

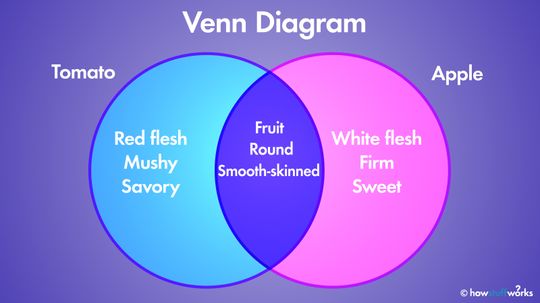
Venn diagrams are an easy way to simplify information and visualize relationships between concepts or sets of data.

By Jesslyn Shields & Sascha Bos

It's easy to make a Mobius strip with some paper and tape, but your mind will be blown by the mathematical concepts it unlocks.

By Trevor English

Two lines that are perpendicular to the same line are parallel to each other and will never intersect.

By Mark Mancini

It's an important question, so come with us and we'll show you how to figure it out.

By Jesslyn Shields

A simple math problem may seem to some of us like an inscrutable pile of numbers and symbols, just waiting to trip us up. PEMDAS to the rescue!

By Mark Mancini & Desiree Bowie

Can you name even one female mathematician? Don't worry if you can't. That just means you need to read our article on five famous female mathematicians to up your cred.

By Dave Roos

Spanish researchers recently uncovered a new geometric shape that allows human tissue to curve. But how?

By Robert Lamb

The Pythagorean theorem, which explains how to calculate the longest side of a right-angled triangle, is an ancient mathematical statement that still buttresses modern-day construction, aviation and even how we navigate through traffic.

By Patrick J. Kiger & Talon Homer

We'll show you both a quick and dirty way, and a precise, more complicated formula for converting Celsius to Fahrenheit (and vice versa).

By Sydney Murphy & Austin Henderson

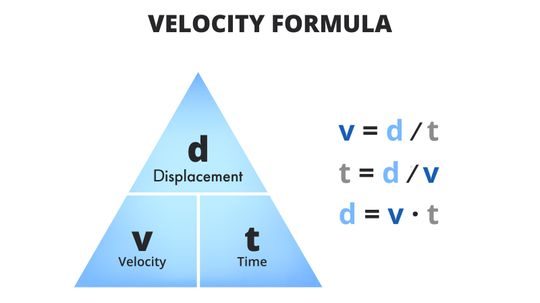
Many people get speed and velocity confused. It's no surprise because the terms are often used interchangeably. But they're not quite the same thing. So how do you find the velocity of an object?

By Mark Mancini

Converting kilogram measurements into pounds is not hard. We'll show you the textbook way plus two quick-and-dirty shortcuts.

By Mark Mancini

Most of the world uses meters, apart from the U.S. and a few other countries. So what's an easy way to convert from meters to feet and vice versa?

By Mark Mancini

Both degrees and radians represent the measure of an angle in geometry. So, how do you convert one to the other?

By Mark Mancini

You can find the distance between two points by using the distance formula. It's an application of the Pythagorean theorem. Remember that from high school algebra?

By Mark Mancini & Desiree Bowie

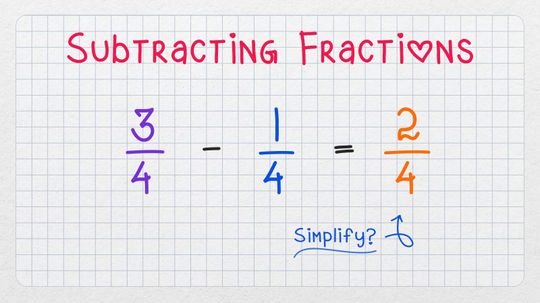
The very idea of trying to subtract one fraction from another may send you into convulsions of fear, but don't worry - we'll show you how.

By Jesslyn Shields & Austin Henderson

Want to know the area of your pizza or the kitchen you're eating it in? Come on, and we'll show you how to figure it out with an area formula.

By Thomas Harlander

We take the mystery out of reporting the percent error correctly and show you how to use it in real life.

By Mark Mancini