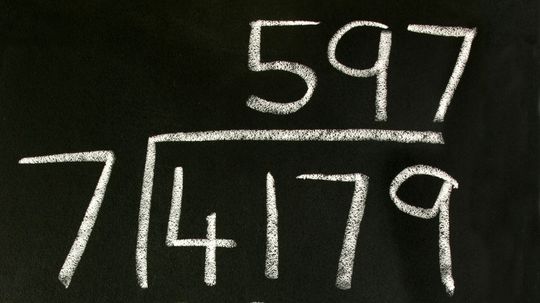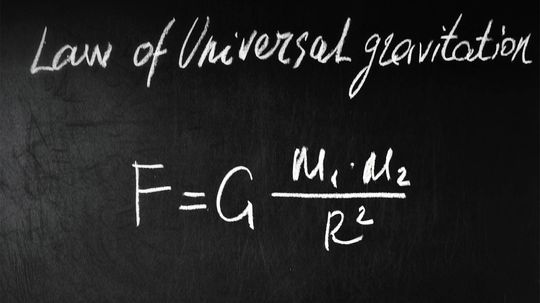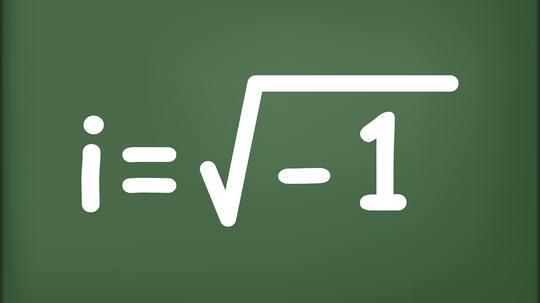Math Concepts

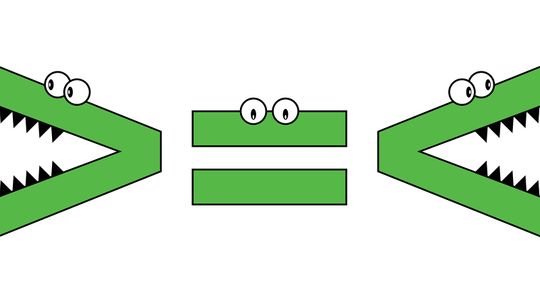
Greater than, less than, equal to: These terms are mathematical expressions that allow the user to compare two numbers or equations. Once you've become familiar with these terms - and the symbols used to represent them - you'll be able to apply them to various math problems.

By Zach Taras

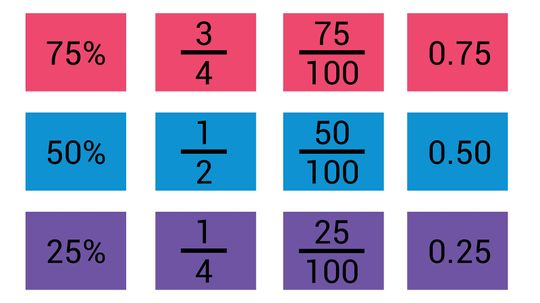
As you might recall from math class, fractions and decimals are two different ways of representing the same thing. A third option, percentages, is a close cousin of decimals. However, making use of this knowledge requires knowing how to convert one into the other.

By Zach Taras

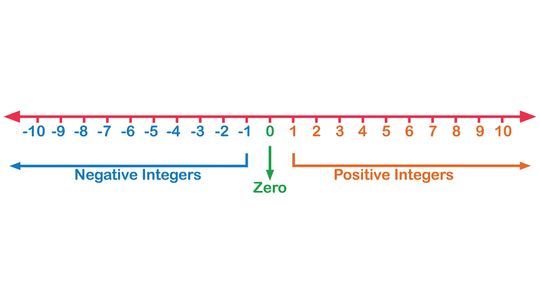
A number line is a pictorial representation of real numbers. It is most commonly used in elementary math classes to help students compare numbers and perform arithmetic operations like addition, subtraction, division and multiplication.

By Mitch Ryan

Mean, median, mode and sometimes range, are all different methods for finding probability distribution in statistics. Range can be a helpful yardstick when calculating data values that are close together, but it can quickly become confusing if there is a wide gap between the smallest value and the largest number.

By Mitch Ryan

As a child, when trying to come up with the biggest number possible, you might have said "infinity plus one." While technically infinity is the largest number because you cannot run out of numbers, the biggest numbers that we know of are still difficult to count but a bit more quantifiable.

By Yara Simón

Do you need to calculate the rate at which something changes over time? Whether it's the change in the x-value over the change in the y-value of a line on a graph, or the distance travelled by a car over the course of an hour-long drive, you'll need a rate of change formula.

By Sascha Bos

Physicists use the displacement formula to find an object's change in position. It sounds simple, but calculating displacement can quickly get complicated.

By Sascha Bos

Frequency is a fundamental concept when you're talking about waves, whether that means electromagnetic waves like radio waves and visible light, or mechanical vibrations like sound waves.

By Marie Look

The wavelength formula is a fundamental concept in physics, particularly in the study of waves and electromagnetic radiation.

By Yara Simón

In math, few skills are as practical as knowing how to do long division. It's the art of breaking down complex problems into manageable steps, making it an essential tool for students and adults alike.

By Desiree Bowie

We get it: You need help with the parabola equation because those graphs won't draw themselves. Here's how to draw a parabola from an equation.

By Yara Simón

Trying to figure out whether your research problem would benefit from qualitative vs. quantitative data? Learn about the differences and uses of each.

By Yara Simón

Distinguishing between discrete vs. continuous data and situations that call for each data type is important in ensuring you get your desired results.

By Marie Look

Whether you're a math whiz or not, there are some pretty cool number theories, beliefs and coincidences to appreciate. How down with digits are you?

By Alia Hoyt

The scutoid is kind of like the Higgs boson. Researchers theorized the new shape existed. And then they went looking for it.

The Fibonacci sequence has been a numerical sequence for millennia. But what does it have to do with sunflower seeds or rabbits?

By Robert Lamb & Jesslyn Shields

Whether the circle is as big as planet Mars or as small as a tennis ball, the ratio of its circumference divided by its diameter will always equal pi (3.14). But why?

By Marshall Brain, Dave Roos & Austin Henderson

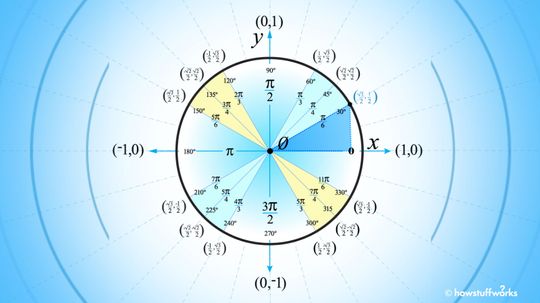
A unit circle is an important part of trigonometry and can define right angle relationships known as sine, cosine and tangent.

By Nokware Knight & Austin Henderson

A multiplication table is an easy-to-use grid of numbers that can help you learn to multiply quickly by using the chart and, eventually, your memory.

By Kristen Hall-Geisler & Austin Henderson

Sir Isaac Newton's Law of Universal Gravitation helps put the laws of gravity into a mathematical formula. And the gravitational constant is the "G" in that formula.

By Mark Mancini

Bayes' theorem describes the probability of an event, based on prior knowledge of conditions that might be related to the event. Sounds intimidating, but we'll walk you through it.

By Mark Mancini

Science requires that we make guesses, which is why we have confidence intervals.

By Jesslyn Shields

An imaginary number is a value that's the square root of a negative number. It can't exist on a one-dimensional number line. We'll explain.

By Patrick J. Kiger & Austin Henderson

Numerators and denominators, oh my! It sounds complicated, but learning how to multiply fractions is easy. It just takes three simple steps.

By Jesslyn Shields

Dividing fractions is easy once you learn a couple of rules and remember three words - keep, change and flip.

By Jesslyn Shields